
Question Number 210324 by Ghisom last updated on 06/Aug/24

$$\mathrm{rationalize}\:\mathrm{the}\:\mathrm{denominator}: \\ $$$$\frac{\mathrm{1}}{{a}+{b}^{\mathrm{1}/\mathrm{3}} +{c}^{\mathrm{1}/\mathrm{3}} } \\ $$
Commented by Spillover last updated on 06/Aug/24
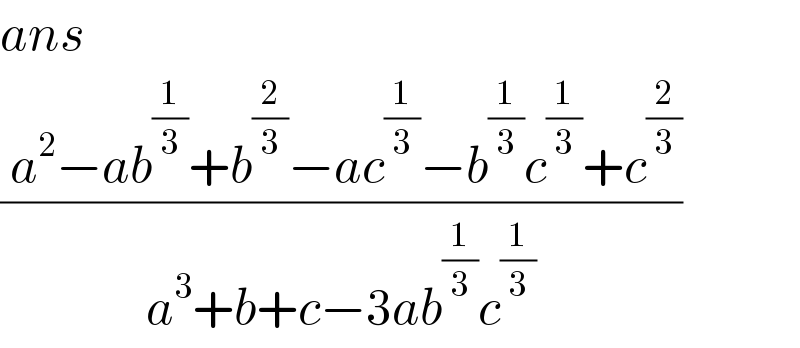
$${ans}\: \\ $$$$\frac{\:{a}^{\mathrm{2}} −{ab}^{\frac{\mathrm{1}}{\mathrm{3}}} +{b}^{\frac{\mathrm{2}}{\mathrm{3}}} −{ac}^{\frac{\mathrm{1}}{\mathrm{3}}} −{b}^{\frac{\mathrm{1}}{\mathrm{3}}} {c}^{\frac{\mathrm{1}}{\mathrm{3}}} +{c}^{\frac{\mathrm{2}}{\mathrm{3}}} }{{a}^{\mathrm{3}} +{b}+{c}−\mathrm{3}{ab}^{\frac{\mathrm{1}}{\mathrm{3}}} {c}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:\:\: \\ $$
Commented by Ghisom last updated on 06/Aug/24
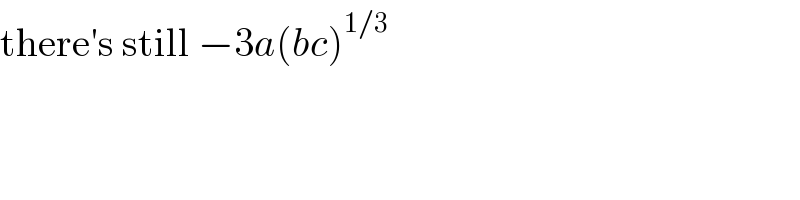
$$\mathrm{there}'\mathrm{s}\:\mathrm{still}\:−\mathrm{3}{a}\left({bc}\right)^{\mathrm{1}/\mathrm{3}} \\ $$
Answered by Frix last updated on 08/Aug/24
![1. Expand with [ω=−(1/2)+((√3)/2)i] (a+ωb^(1/3) +ω^2 c^(1/3) )(a+ω^2 b^(1/3) +ωc^(1/3) )= =(a^2 −a(b^(1/3) +c^(1/3) )+b^(2/3) −b^(1/3) c^(1/3) +c^(2/3) ) The denominator now is (a^3 +b+c−3ab^(1/3) c^(1/3) )=(p−q^(1/3) ) ⇒ 2. Expand with [p=a^3 +b+c∧q=27a^3 bc] (p^2 +pq^(1/3) +q^(2/3) ) to get p^3 −q The denominator now is a^9 +3a^6 (b+c)+3a^3 (b^2 −7bc+c^2 )+(b+c)^3 [Works even with a=α^(1/3) ]](Q210379.png)
$$\mathrm{1}.\:\mathrm{Expand}\:\mathrm{with}\:\:\:\:\:\left[\omega=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right] \\ $$$$\left({a}+\omega{b}^{\frac{\mathrm{1}}{\mathrm{3}}} +\omega^{\mathrm{2}} {c}^{\frac{\mathrm{1}}{\mathrm{3}}} \right)\left({a}+\omega^{\mathrm{2}} {b}^{\frac{\mathrm{1}}{\mathrm{3}}} +\omega{c}^{\frac{\mathrm{1}}{\mathrm{3}}} \right)= \\ $$$$=\left({a}^{\mathrm{2}} −{a}\left({b}^{\frac{\mathrm{1}}{\mathrm{3}}} +{c}^{\frac{\mathrm{1}}{\mathrm{3}}} \right)+{b}^{\frac{\mathrm{2}}{\mathrm{3}}} −{b}^{\frac{\mathrm{1}}{\mathrm{3}}} {c}^{\frac{\mathrm{1}}{\mathrm{3}}} +{c}^{\frac{\mathrm{2}}{\mathrm{3}}} \right) \\ $$$$\mathrm{The}\:\mathrm{denominator}\:\mathrm{now}\:\mathrm{is} \\ $$$$\left({a}^{\mathrm{3}} +{b}+{c}−\mathrm{3}{ab}^{\frac{\mathrm{1}}{\mathrm{3}}} {c}^{\frac{\mathrm{1}}{\mathrm{3}}} \right)=\left({p}−{q}^{\frac{\mathrm{1}}{\mathrm{3}}} \right) \\ $$$$\Rightarrow \\ $$$$\mathrm{2}.\:\mathrm{Expand}\:\mathrm{with}\:\:\:\:\:\left[{p}={a}^{\mathrm{3}} +{b}+{c}\wedge{q}=\mathrm{27}{a}^{\mathrm{3}} {bc}\right] \\ $$$$\left({p}^{\mathrm{2}} +{pq}^{\frac{\mathrm{1}}{\mathrm{3}}} +{q}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)\:\mathrm{to}\:\mathrm{get}\:{p}^{\mathrm{3}} −{q} \\ $$$$\mathrm{The}\:\mathrm{denominator}\:\mathrm{now}\:\mathrm{is} \\ $$$${a}^{\mathrm{9}} +\mathrm{3}{a}^{\mathrm{6}} \left({b}+{c}\right)+\mathrm{3}{a}^{\mathrm{3}} \left({b}^{\mathrm{2}} −\mathrm{7}{bc}+{c}^{\mathrm{2}} \right)+\left({b}+{c}\right)^{\mathrm{3}} \\ $$$$ \\ $$$$\left[\mathrm{Works}\:\mathrm{even}\:\mathrm{with}\:{a}=\alpha^{\frac{\mathrm{1}}{\mathrm{3}}} \right] \\ $$
Commented by Ghisom last updated on 14/Aug/24

$$\mathrm{thank}\:\mathrm{you} \\ $$
