
Question Number 196013 by pticantor last updated on 15/Aug/23

$${quel}\:{est}\:{la}\:{transformer}\:{de}\:{Fourier}\:{de}\:{la}\:{fonction} \\ $$$${suivante}: \\ $$$${f}\left({x}\right)=\boldsymbol{{e}}^{−\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\boldsymbol{{F}}{ind}\:{the}\:{Fourier}\:{transform}\:{of}\:{the}\: \\ $$$${following}\:{fonction}. \\ $$
Answered by witcher3 last updated on 16/Aug/23
![∫_(−∞) ^∞ e^(−ixt) e^(−(x^2 /2)) dx =∫_(−∞) ^∞ e^(−(1/2)(x^2 +2ixt)) dx =∫_(−∞) ^∞ e^(−(1/2)(x+it)^2 −(t^2 /2)) dx =e^(−(t^2 /2)) ∫_(−∞) ^∞ e^(−(1/2)(x+it)^2 ) dx e^(−(t^2 /2)) ∫_(−∞+it) ^(∞+it) e^(−(1/2)y^2 ) dy D=]−R,R[∪[R,R+it]∪[R+it,−R+it]∪[−R+it,−R] ∫_D e^(−(1/2)y^2 ) dy=0 lim_(R→∞) ∣∫_(+_− R) ^(+_− R+it) e^(−(y^2 /2)) dy∣≤lim_(R→∞) ∣te^(−(1/2)(R^2 +t^2 )) ∣=0 ⇒∫_(−∞+it) ^(∞+it) e^(−(y^2 /2)) dy=∫_(−∞) ^∞ e^(−(y^2 /2)) = 2∫_0 ^∞ e^(−(y^2 /2)) dy=(√2)∫_0 ^∞ e^(−x) .x^(−(1/2)) dx =(√2).Γ((1/2))=(√(2π)) F(e^(−(x^2 /2)) )=(√(2π))e^(−(t^2 /2)) .](Q196019.png)
$$\int_{−\infty} ^{\infty} \mathrm{e}^{−\mathrm{ixt}} \mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \mathrm{dx} \\ $$$$=\int_{−\infty} ^{\infty} \mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2ixt}\right)} \mathrm{dx} \\ $$$$=\int_{−\infty} ^{\infty} \mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}+\mathrm{it}\right)^{\mathrm{2}} −\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}} \mathrm{dx} \\ $$$$=\mathrm{e}^{−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}} \int_{−\infty} ^{\infty} \mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}+\mathrm{it}\right)^{\mathrm{2}} } \mathrm{dx} \\ $$$$\mathrm{e}^{−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}} \int_{−\infty+\mathrm{it}} ^{\infty+\mathrm{it}} \mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{y}^{\mathrm{2}} } \mathrm{dy} \\ $$$$\left.\mathrm{D}=\right]−\mathrm{R},\mathrm{R}\left[\cup\left[\mathrm{R},\mathrm{R}+\mathrm{it}\right]\cup\left[\mathrm{R}+\mathrm{it},−\mathrm{R}+\mathrm{it}\right]\cup\left[−\mathrm{R}+\mathrm{it},−\mathrm{R}\right]\right. \\ $$$$\int_{\mathrm{D}} \mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{y}^{\mathrm{2}} } \mathrm{dy}=\mathrm{0} \\ $$$$\underset{\mathrm{R}\rightarrow\infty} {\mathrm{lim}}\mid\int_{\underset{−} {+}\mathrm{R}} ^{\underset{−} {+}\mathrm{R}+\mathrm{it}} \mathrm{e}^{−\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{2}}} \mathrm{dy}\mid\leqslant\underset{\mathrm{R}\rightarrow\infty} {\mathrm{lim}}\mid\mathrm{te}^{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{R}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} \right)} \mid=\mathrm{0} \\ $$$$\Rightarrow\int_{−\infty+\mathrm{it}} ^{\infty+\mathrm{it}} \mathrm{e}^{−\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{2}}} \mathrm{dy}=\int_{−\infty} ^{\infty} \mathrm{e}^{−\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{2}}} = \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{2}}} \mathrm{dy}=\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{x}} .\mathrm{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{dx} \\ $$$$=\sqrt{\mathrm{2}}.\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\mathrm{2}\pi} \\ $$$$\mathcal{F}\left(\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \right)=\sqrt{\mathrm{2}\pi}\mathrm{e}^{−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}} . \\ $$
Commented by witcher3 last updated on 16/Aug/23
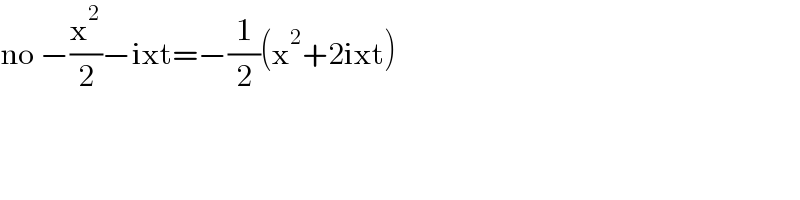
$$\mathrm{no}\:−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{ixt}=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2ixt}\right) \\ $$
Commented by pticantor last updated on 16/Aug/23
$${in}\:{the}\:\mathrm{2}{nd}\:{line}\:{you}\:{make}\:{some}\:{mistake}\:{look}\:{well} \\ $$
Commented by pticantor last updated on 16/Aug/23

$${the}\:{fourier}\:{tranformation}\:{formule}\:{is}: \\ $$$${F}\left({f}\right)\left({t}\right)=\int_{−\infty} ^{+\infty} {e}^{−\mathrm{2}\pi{ixt}} {f}\left({x}\right){dx}\:!!! \\ $$
Commented by witcher3 last updated on 17/Aug/23

$$\mathrm{Ah}\:\mathrm{yes}\:\mathrm{forget}\:\mathrm{the}\:\mathrm{formula}\: \\ $$$$\mathrm{i}\:\mathrm{thougth}\:\mathrm{it}\:\mathrm{e}^{−\mathrm{ixt}\:\:} \mathrm{sorry} \\ $$
