
Previous in Differential Equation Next in Differential Equation
Question Number 21252 by youssoufab last updated on 17/Sep/17
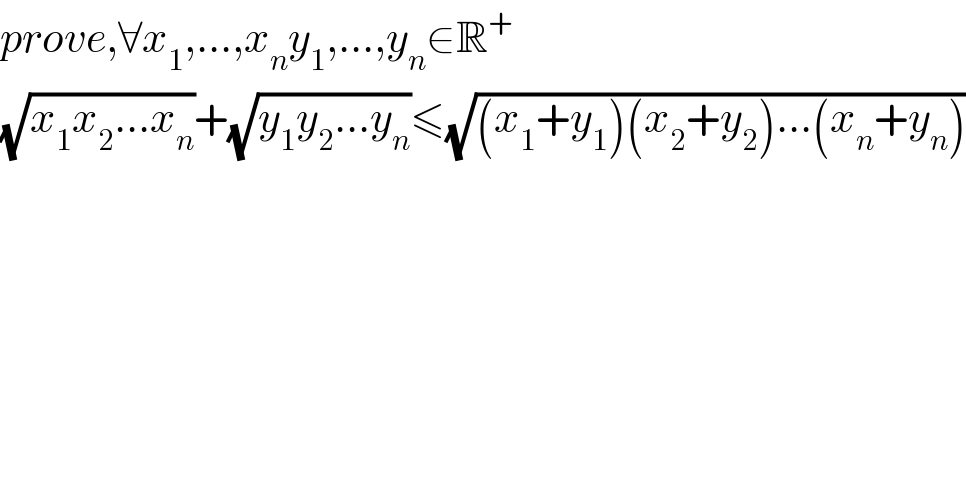
$${prove},\forall{x}_{\mathrm{1}} ,...,{x}_{{n}} {y}_{\mathrm{1}} ,...,{y}_{{n}} \in\mathbb{R}^{+} \\ $$$$\sqrt{{x}_{\mathrm{1}} {x}_{\mathrm{2}} ...{x}_{{n}} }+\sqrt{{y}_{\mathrm{1}} {y}_{\mathrm{2}} ...{y}_{{n}} }\leqslant\sqrt{\left({x}_{\mathrm{1}} +{y}_{\mathrm{1}} \right)\left({x}_{\mathrm{2}} +{y}_{\mathrm{2}} \right)...\left({x}_{{n}} +{y}_{{n}} \right)} \\ $$
