
Question Number 8022 by Nayon last updated on 28/Sep/16
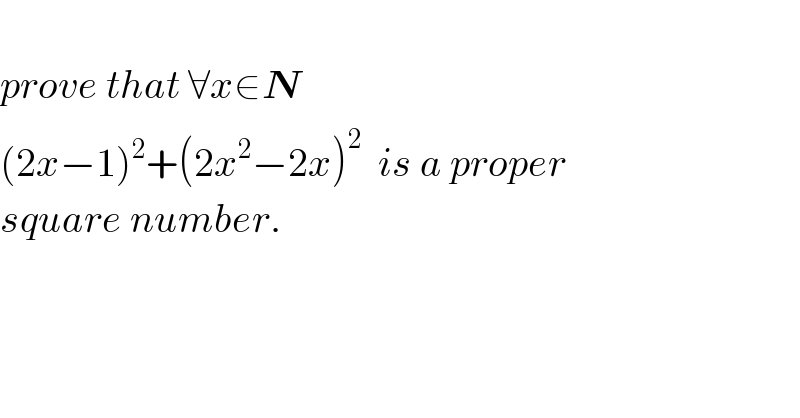
$$ \\ $$$${prove}\:{that}\:\forall{x}\in\boldsymbol{{N}}\: \\ $$$$\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}\right)^{\mathrm{2}} \:\:{is}\:{a}\:{proper} \\ $$$${square}\:{number}. \\ $$
Commented by prakash jain last updated on 28/Sep/16
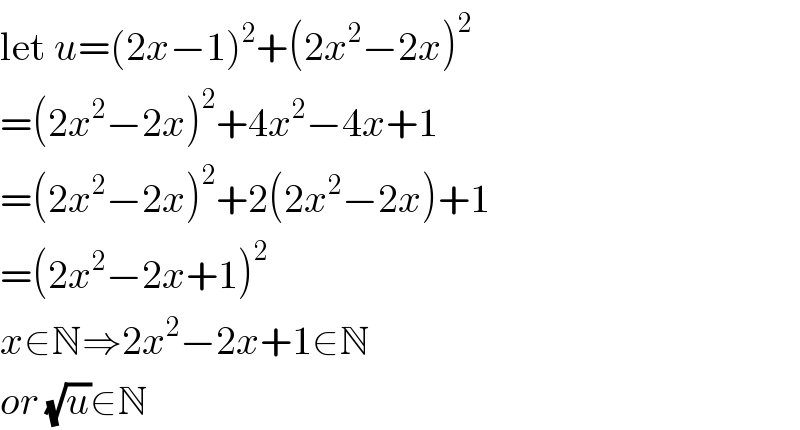
$$\mathrm{let}\:{u}=\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}\right)^{\mathrm{2}} \\ $$$$=\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}\right)^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1} \\ $$$$=\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}\right)+\mathrm{1} \\ $$$$=\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${x}\in\mathbb{N}\Rightarrow\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\in\mathbb{N} \\ $$$${or}\:\sqrt{{u}}\in\mathbb{N} \\ $$
Answered by prakash jain last updated on 02/Oct/16
$$\mathrm{answer}\:\mathrm{in}\:\mathrm{comments} \\ $$
