Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 132475 by Study last updated on 14/Feb/21

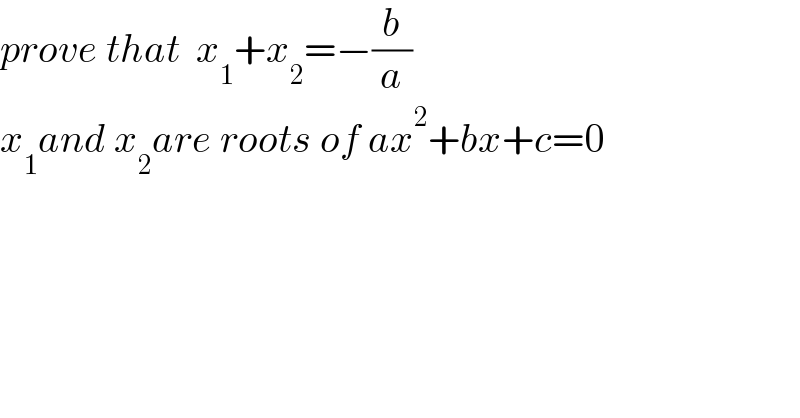
prove that x_1 +x_2 =−(b/a) x_1 and x_2 are roots of ax^2 +bx+c=0

$${prove}\:{that}\:\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} =−\frac{{b}}{{a}} \\ $$$${x}_{\mathrm{1}} {and}\:{x}_{\mathrm{2}} {are}\:{roots}\:{of}\:{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$

Commented by MJS_new last updated on 14/Feb/21

it′s just the solution formula again. solve the quadratic and add the solutions. where′s the problem?

$$\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{formula}\:\mathrm{again}.\:\mathrm{solve} \\ $$$$\mathrm{the}\:\mathrm{quadratic}\:\mathrm{and}\:\mathrm{add}\:\mathrm{the}\:\mathrm{solutions}.\:\mathrm{where}'\mathrm{s} \\ $$$$\mathrm{the}\:\mathrm{problem}? \\ $$

Commented by EDWIN88 last updated on 14/Feb/21

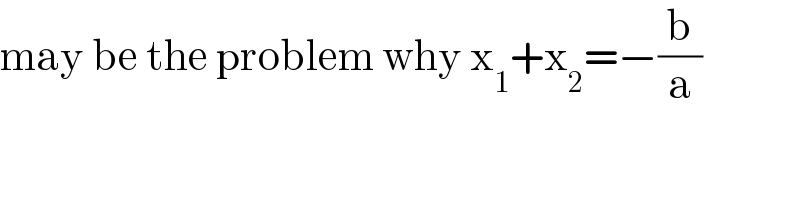
may be the problem why x_1 +x_2 =−(b/a)

$$\mathrm{may}\:\mathrm{be}\:\mathrm{the}\:\mathrm{problem}\:\mathrm{why}\:\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} =−\frac{\mathrm{b}}{\mathrm{a}} \\ $$

Commented by MJS_new last updated on 14/Feb/21

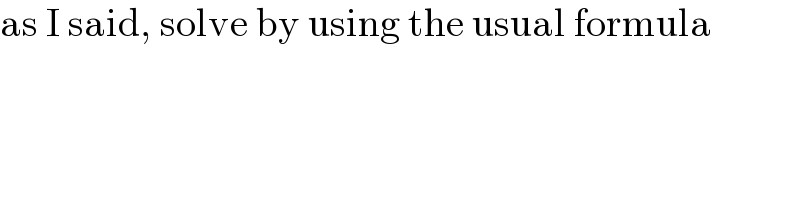
as I said, solve by using the usual formula

$$\mathrm{as}\:\mathrm{I}\:\mathrm{said},\:\mathrm{solve}\:\mathrm{by}\:\mathrm{using}\:\mathrm{the}\:\mathrm{usual}\:\mathrm{formula} \\ $$

Commented by EDWIN88 last updated on 14/Feb/21

yes

$$\mathrm{yes} \\ $$

Answered by rs4089 last updated on 14/Feb/21

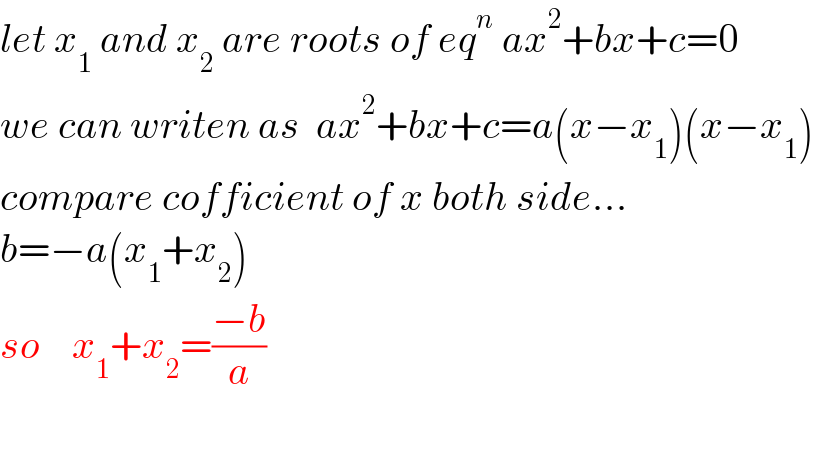
let x_1 and x_2 are roots of eq^n ax^2 +bx+c=0 we can writen as ax^2 +bx+c=a(x−x_1 )(x−x_1 ) compare cofficient of x both side... b=−a(x_1 +x_2 ) so x_1 +x_2 =((−b)/a)

$${let}\:{x}_{\mathrm{1}} \:{and}\:{x}_{\mathrm{2}} \:{are}\:{roots}\:{of}\:{eq}^{{n}} \:{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$${we}\:{can}\:{writen}\:{as}\:\:{ax}^{\mathrm{2}} +{bx}+{c}={a}\left({x}−{x}_{\mathrm{1}} \right)\left({x}−{x}_{\mathrm{1}} \right) \\ $$$${compare}\:{cofficient}\:{of}\:{x}\:{both}\:{side}... \\ $$$${b}=−{a}\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right) \\ $$$${so}\:\:\:\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} =\frac{−{b}}{{a}} \\ $$$$ \\ $$

Answered by physicstutes last updated on 14/Feb/21

Or begin with the general solution to the quadratic: x = ((−b±(√(b^2 −4ac)))/(2a)) say, x_1 = ((−b+(√(b^2 −4ac)))/(2a)) and x_2 =((−b−(√(b^2 −4ac)))/(2a)) x_1 + x_2 = ((−b+(√(b^2 −4ac)))/(2a)) + ((−b−(√(b^2 −2ac)))/(2a)) = ((−b+(√(b^2 −4a4)) −b −(√(b^2 −4ac)))/(2a)) x_1 + x_2 = ((−b−b)/(2a)) = ((−b)/a) hence x_1 + x_2 =−(b/a) similarly it can be shown that x_1 x_2 = (c/a)

$$\mathrm{Or}\:\mathrm{begin}\:\mathrm{with}\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{the}\:\mathrm{quadratic}: \\ $$$$\:{x}\:=\:\frac{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}} \\ $$$$\mathrm{say},\:{x}_{\mathrm{1}} \:=\:\frac{−{b}+\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}}\:\mathrm{and}\:{x}_{\mathrm{2}} \:=\frac{−{b}−\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}} \\ $$$${x}_{\mathrm{1}} +\:{x}_{\mathrm{2}} \:=\:\frac{−{b}+\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}}\:+\:\frac{−{b}−\sqrt{{b}^{\mathrm{2}} −\mathrm{2}{ac}}}{\mathrm{2}{a}}\:=\:\frac{−{b}+\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{a}\mathrm{4}}\:−{b}\:−\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}} \\ $$$$\:{x}_{\mathrm{1}} \:+\:{x}_{\mathrm{2}} \:=\:\frac{−{b}−{b}}{\mathrm{2}{a}}\:=\:\frac{−{b}}{{a}} \\ $$$$\mathrm{hence}\:{x}_{\mathrm{1}} \:+\:{x}_{\mathrm{2}} \:=−\frac{{b}}{{a}} \\ $$$$\mathrm{similarly}\:\mathrm{it}\:\mathrm{can}\:\mathrm{be}\:\mathrm{shown}\:\mathrm{that}\:\:{x}_{\mathrm{1}} {x}_{\mathrm{2}} \:=\:\frac{{c}}{{a}} \\ $$

Commented by MJS_new last updated on 14/Feb/21

that′s exactly what I recommended if we answer the easiest questions, people wil never learn anything. you can do all their thinking − at least all their homework − for them for all eternity.

$$\mathrm{that}'\mathrm{s}\:\mathrm{exactly}\:\mathrm{what}\:\mathrm{I}\:\mathrm{recommended} \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{answer}\:\mathrm{the}\:\mathrm{easiest}\:\mathrm{questions},\:\mathrm{people} \\ $$$$\mathrm{wil}\:\mathrm{never}\:\mathrm{learn}\:\mathrm{anything}.\:\mathrm{you}\:\mathrm{can}\:\mathrm{do}\:\mathrm{all} \\ $$$$\mathrm{their}\:\mathrm{thinking}\:−\:\mathrm{at}\:\mathrm{least}\:\mathrm{all}\:\mathrm{their}\:\mathrm{homework}\:− \\ $$$$\mathrm{for}\:\mathrm{them}\:\mathrm{for}\:\mathrm{all}\:\mathrm{eternity}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com