
Question Number 132055 by Study last updated on 10/Feb/21
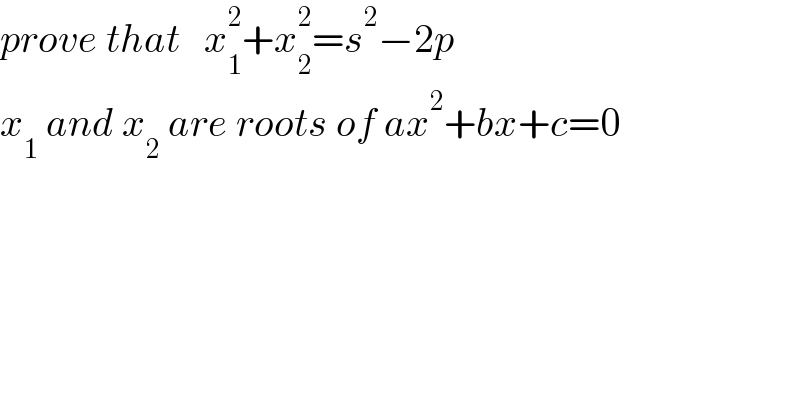
$${prove}\:{that}\:\:\:{x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} ={s}^{\mathrm{2}} −\mathrm{2}{p} \\ $$$${x}_{\mathrm{1}} \:{and}\:{x}_{\mathrm{2}} \:{are}\:{roots}\:{of}\:{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$
Commented by JDamian last updated on 10/Feb/21
what are s and p?
Commented by rhgy767iu last updated on 10/Feb/21
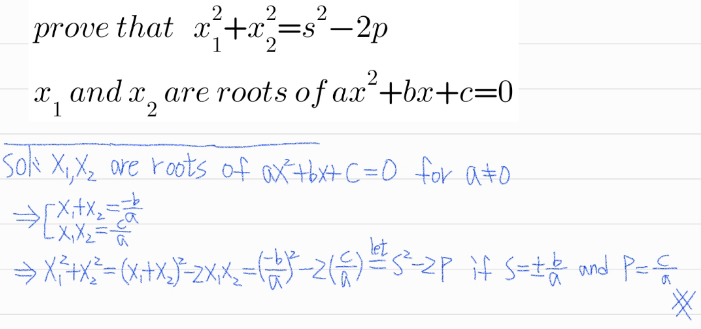
Answered by MJS_new last updated on 11/Feb/21
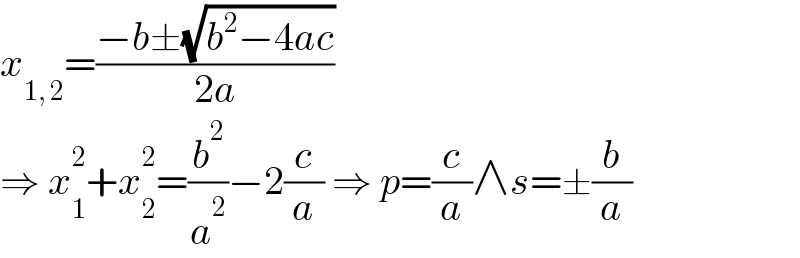
$${x}_{\mathrm{1},\:\mathrm{2}} =\frac{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}} \\ $$$$\Rightarrow\:{x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\mathrm{2}\frac{{c}}{{a}}\:\Rightarrow\:{p}=\frac{{c}}{{a}}\wedge{s}=\pm\frac{{b}}{{a}} \\ $$
