
Question Number 181570 by SANOGO last updated on 26/Nov/22
![prove that:xε]−1,1[ Σ_(n=1) ^(+oo) (x^n /n)=−ln(1−x)](Q181570.png)
$$\left.{prove}\:{that}:{x}\epsilon\right]−\mathrm{1},\mathrm{1}\left[\right. \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+{oo}} {\sum}}\frac{{x}^{{n}} }{{n}}=−{ln}\left(\mathrm{1}−{x}\right) \\ $$
Answered by mr W last updated on 27/Nov/22
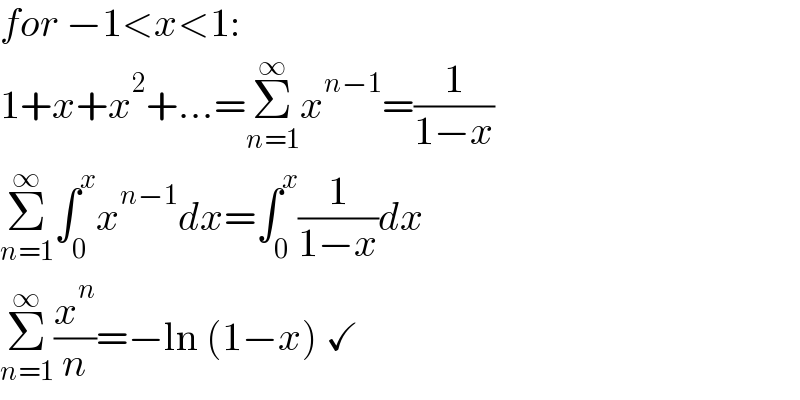
$${for}\:−\mathrm{1}<{x}<\mathrm{1}: \\ $$$$\mathrm{1}+{x}+{x}^{\mathrm{2}} +...=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{{x}} {x}^{{n}−\mathrm{1}} {dx}=\int_{\mathrm{0}} ^{{x}} \frac{\mathrm{1}}{\mathrm{1}−{x}}{dx} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}}=−\mathrm{ln}\:\left(\mathrm{1}−{x}\right)\:\checkmark \\ $$
Commented by SANOGO last updated on 27/Nov/22
$${thank}\:{you} \\ $$
