
Previous in Relation and Functions Next in Relation and Functions
Question Number 29842 by abdo imad last updated on 12/Feb/18
![prove that ∀ x∈]0,1[ (1/(Γ(x).Γ(1−x)))=x Π_(n=1) ^∞ (1−(x^2 /n^2 )).](Q29842.png)
$$\left.{prove}\:{that}\:\forall\:{x}\in\right]\mathrm{0},\mathrm{1}\left[\:\:\:\:\:\:\frac{\mathrm{1}}{\Gamma\left({x}\right).\Gamma\left(\mathrm{1}−{x}\right)}={x}\:\prod_{{n}=\mathrm{1}} ^{\infty} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right).\right. \\ $$
Commented by abdo imad last updated on 12/Feb/18
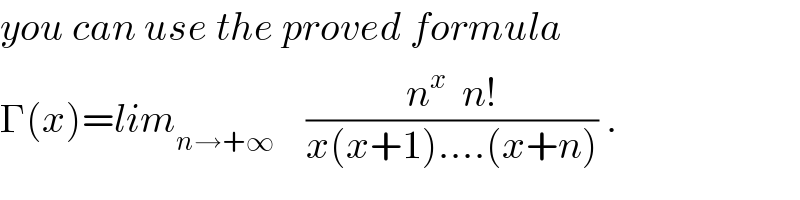
$${you}\:{can}\:{use}\:{the}\:{proved}\:{formula} \\ $$$$\Gamma\left({x}\right)={lim}_{{n}\rightarrow+\infty} \:\:\:\:\frac{{n}^{{x}} \:\:{n}!}{{x}\left({x}+\mathrm{1}\right)....\left({x}+{n}\right)}\:. \\ $$
