
Question Number 78447 by arkanmath7@gmail.com last updated on 17/Jan/20
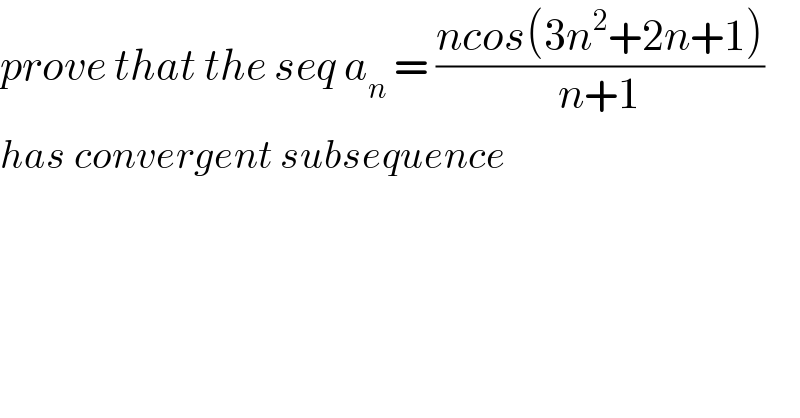
$${prove}\:{that}\:{the}\:{seq}\:{a}_{{n}} \:=\:\frac{{ncos}\left(\mathrm{3}{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}\right)}{{n}+\mathrm{1}} \\ $$$${has}\:{convergent}\:{subsequence} \\ $$
Answered by mind is power last updated on 17/Jan/20
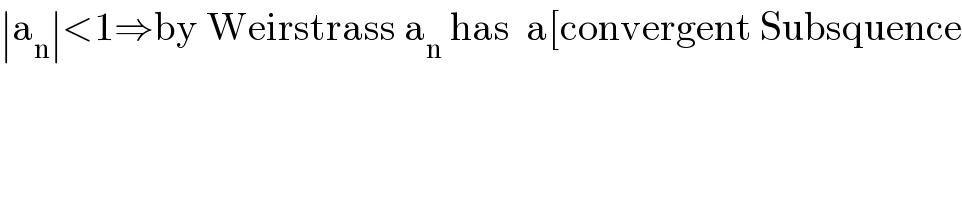
$$\mid\mathrm{a}_{\mathrm{n}} \mid<\mathrm{1}\Rightarrow\mathrm{by}\:\mathrm{Weirstrass}\:\mathrm{a}_{\mathrm{n}} \:\mathrm{has}\:\:\mathrm{a}\left[\mathrm{convergent}\:\mathrm{Subsquence}\right. \\ $$
