
Question Number 113769 by deleteduser12 last updated on 15/Sep/20
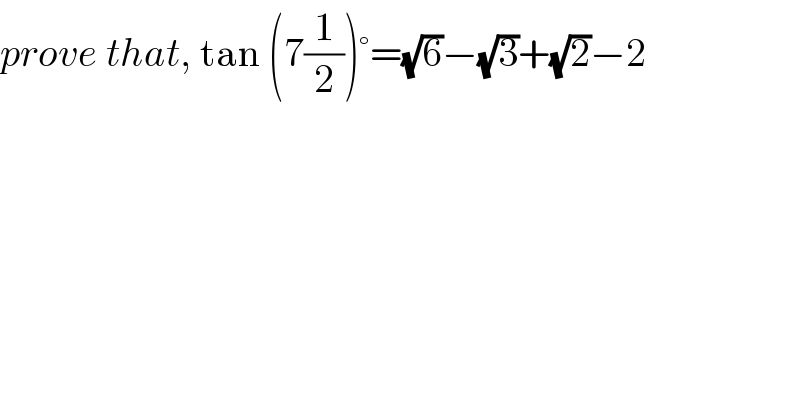
$${prove}\:{that},\:\mathrm{tan}\:\left(\mathrm{7}\frac{\mathrm{1}}{\mathrm{2}}\right)°=\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}−\mathrm{2} \\ $$
Answered by Dwaipayan Shikari last updated on 15/Sep/20
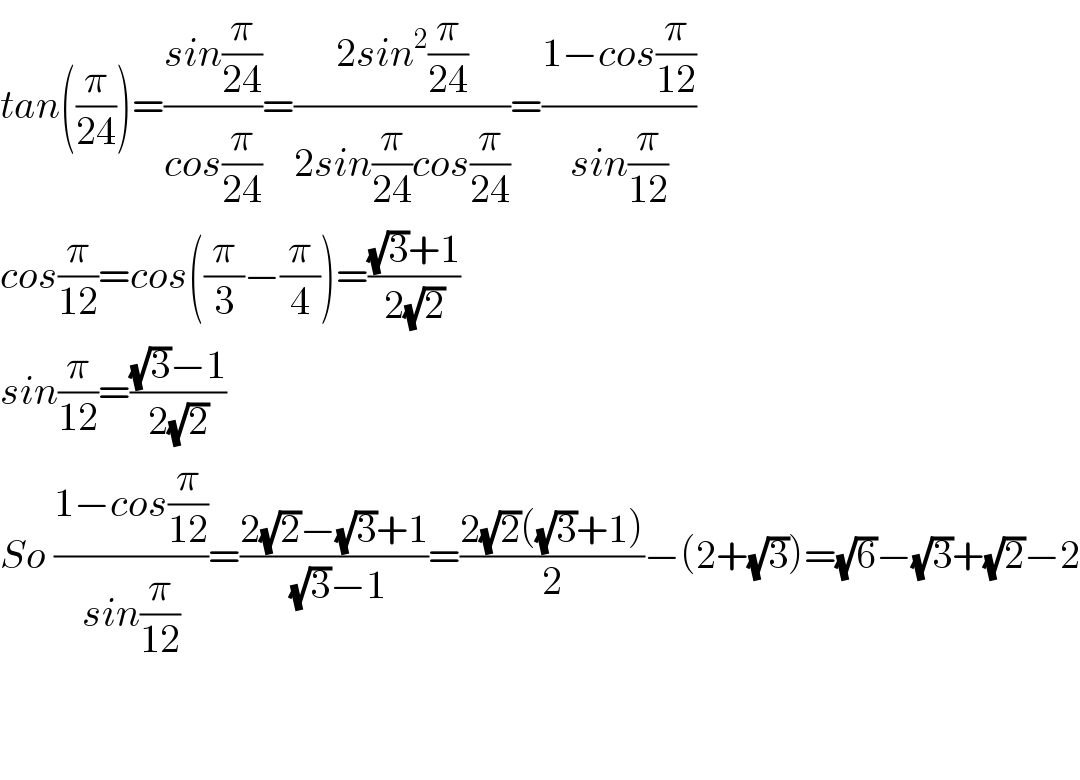
$${tan}\left(\frac{\pi}{\mathrm{24}}\right)=\frac{{sin}\frac{\pi}{\mathrm{24}}}{{cos}\frac{\pi}{\mathrm{24}}}=\frac{\mathrm{2}{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{24}}}{\mathrm{2}{sin}\frac{\pi}{\mathrm{24}}{cos}\frac{\pi}{\mathrm{24}}}=\frac{\mathrm{1}−{cos}\frac{\pi}{\mathrm{12}}}{{sin}\frac{\pi}{\mathrm{12}}} \\ $$$${cos}\frac{\pi}{\mathrm{12}}={cos}\left(\frac{\pi}{\mathrm{3}}−\frac{\pi}{\mathrm{4}}\right)=\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${sin}\frac{\pi}{\mathrm{12}}=\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${So}\:\frac{\mathrm{1}−{cos}\frac{\pi}{\mathrm{12}}}{{sin}\frac{\pi}{\mathrm{12}}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}+\mathrm{1}}{\:\sqrt{\mathrm{3}}−\mathrm{1}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)}{\mathrm{2}}−\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)=\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}−\mathrm{2} \\ $$$$ \\ $$$$ \\ $$
Answered by $@y@m last updated on 15/Sep/20

$$\mathrm{tan}\:\mathrm{30}^{\mathrm{o}} =\frac{\mathrm{2tan}\:\mathrm{15}^{\mathrm{o}} }{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{15}^{\mathrm{o}} } \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}=\frac{\mathrm{2}{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\:{where}\:{x}=\mathrm{tan}\:\mathrm{15}^{{o}} \\ $$$$\mathrm{1}−{x}^{\mathrm{2}} =\mathrm{2}\sqrt{\mathrm{3}}{x} \\ $$$${x}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{x}−\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{2}\sqrt{\mathrm{3}}\pm\sqrt{\mathrm{12}+\mathrm{4}}}{\mathrm{2}} \\ $$$${x}=\frac{−\mathrm{2}\sqrt{\mathrm{3}}\pm\mathrm{4}}{\mathrm{2}}=−\sqrt{\mathrm{3}}\pm\mathrm{2} \\ $$$${But}\:\mathrm{tan}\:\mathrm{15}^{{o}} >\mathrm{0} \\ $$$$\therefore\mathrm{tan}\:\mathrm{15}^{{o}} =\mathrm{2}−\sqrt{\mathrm{3}}\:...\left(\mathrm{1}\right) \\ $$$${Similarly}, \\ $$$$\mathrm{tan}\:\mathrm{15}^{\mathrm{o}} =\frac{\mathrm{2tan}\:\left(\mathrm{7}\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{o}} }{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{7}\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{o}} } \\ $$$$\mathrm{2}−\sqrt{\mathrm{3}}=\frac{\mathrm{2}{y}}{\mathrm{1}−{y}^{\mathrm{2}} }\:{where}\:{y}=\mathrm{tan}\:\left(\mathrm{7}\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{o}} \\ $$$$\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){y}^{\mathrm{2}} +\mathrm{2}{y}−\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)=\mathrm{0} \\ $$$${y}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}+\mathrm{4}\left(\mathrm{4}+\mathrm{3}−\mathrm{4}\sqrt{\mathrm{3}}\right)}}{\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} \\ $$$${y}=\frac{−\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{1}+\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)}}{\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)} \\ $$$${y}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{8}−\mathrm{4}\sqrt{\mathrm{3}}}}{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$${y}=\frac{−\mathrm{1}\pm\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}\right)}{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$${But}\:{y}>\mathrm{0} \\ $$$$\therefore\:{y}=\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{2}−\sqrt{\mathrm{3}}}\: \\ $$$$\:{y}=\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{2}−\sqrt{\mathrm{3}}}\:×\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$${y}=\frac{\mathrm{2}\sqrt{\mathrm{6}}−\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}−\sqrt{\mathrm{6}}+\sqrt{\mathrm{18}}−\sqrt{\mathrm{3}}}{\mathrm{2}^{\mathrm{2}} −\sqrt{\mathrm{3}^{\mathrm{2}} }} \\ $$$${y}=\sqrt{\mathrm{6}}−\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}+\mathrm{3}\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}} \\ $$$${y}=\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}−\mathrm{2} \\ $$
