Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 39312 by kunal1234523 last updated on 05/Jul/18

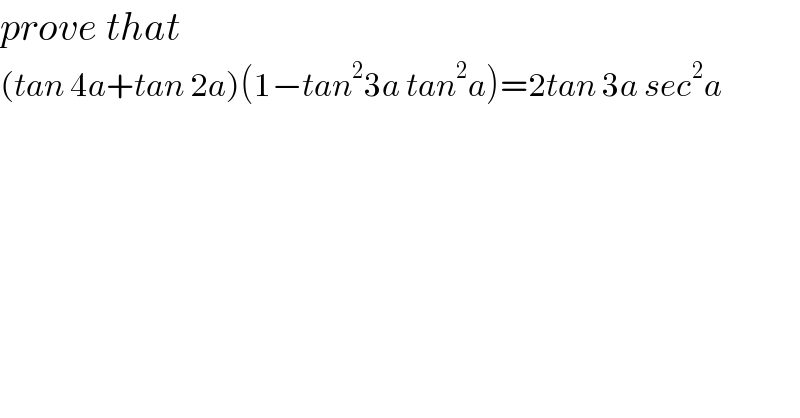
prove that (tan 4a+tan 2a)(1−tan^2 3a tan^2 a)=2tan 3a sec^2 a

$${prove}\:{that} \\ $$$$\left({tan}\:\mathrm{4}{a}+{tan}\:\mathrm{2}{a}\right)\left(\mathrm{1}−{tan}^{\mathrm{2}} \mathrm{3}{a}\:{tan}^{\mathrm{2}} {a}\right)=\mathrm{2}{tan}\:\mathrm{3}{a}\:{sec}^{\mathrm{2}} {a} \\ $$

Answered by kunal1234523 last updated on 05/Jul/18

Commented by kunal1234523 last updated on 05/Jul/18

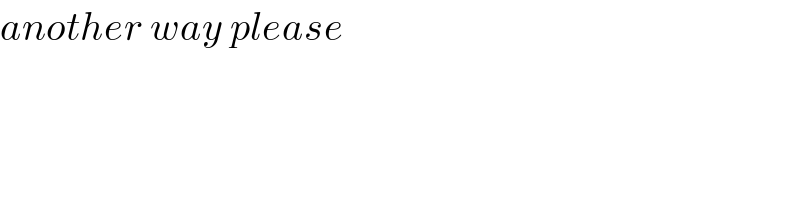
another way please

$${another}\:{way}\:{please} \\ $$

Commented by abdo mathsup 649 cc last updated on 08/Jul/18

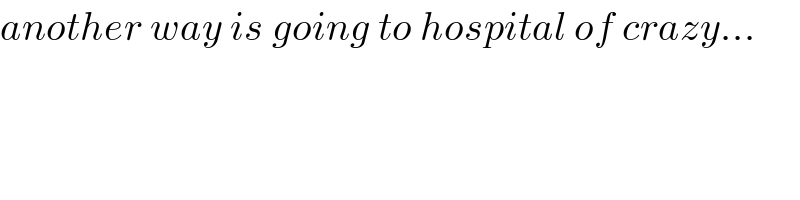
another way is going to hospital of crazy...

$${another}\:{way}\:{is}\:{going}\:{to}\:{hospital}\:{of}\:{crazy}... \\ $$

Answered by MJS last updated on 05/Jul/18

let me write c_n /s_n /t_n for cos nx/sin nx/tan nx (t_4 +t_2 )(1−t_3 ^2 t^2 )=2(t_3 /c^2 ) t_2 +t_4 −t^2 t_3 ^2 t_4 −t^2 t_2 t_3 ^2 =2(t_3 /c^2 ) (s_2 /c_2 )+(s_4 /c_4 )−((s^2 s_3 ^2 s_4 )/(c^2 c_3 ^2 c_4 ))−((s^2 s_2 s_3 ^2 )/(c^2 c_2 c_3 ^2 ))=2(s_3 /(c^2 c_3 )) s_2 c^2 c_3 ^2 c_4 +s_4 c^2 c_2 c_3 ^2 −s^2 s_3 ^2 s_4 c_2 −s^2 s_2 s_3 ^2 c_4 =2s_3 c_2 c_3 c_4 (c^2 c_3 ^2 −s^2 s_3 ^2 )(s_2 c_4 +s_4 c_2 )=2s_3 c_2 c_3 c_4 (c^2 c_3 ^2 −(1−c^2 )(1−c_3 ^2 ))(s_2 c_4 +s_4 c_2 )=2s_3 c_2 c_3 c_4 (c^2 +c_3 ^2 −1)(s_2 c_4 +s_4 c_2 )=2s_3 c_2 c_3 c_4 now use trigonometric formulas until you reach this... ((1/2)(c_2 +c_6 ))(s_6 )=(1/4)(s_4 +s_8 +s_(12) ) ...and again: (1/4)(s_4 +s_8 +s_(12) )=(1/4)(s_4 +s_8 +s_(12) )

$$\mathrm{let}\:\mathrm{me}\:\mathrm{write}\:{c}_{{n}} /{s}_{{n}} /{t}_{{n}} \:\mathrm{for}\:\mathrm{cos}\:{nx}/\mathrm{sin}\:{nx}/\mathrm{tan}\:{nx} \\ $$$$\left({t}_{\mathrm{4}} +{t}_{\mathrm{2}} \right)\left(\mathrm{1}−{t}_{\mathrm{3}} ^{\mathrm{2}} {t}^{\mathrm{2}} \right)=\mathrm{2}\frac{{t}_{\mathrm{3}} }{{c}^{\mathrm{2}} } \\ $$$${t}_{\mathrm{2}} +{t}_{\mathrm{4}} −{t}^{\mathrm{2}} {t}_{\mathrm{3}} ^{\mathrm{2}} {t}_{\mathrm{4}} −{t}^{\mathrm{2}} {t}_{\mathrm{2}} {t}_{\mathrm{3}} ^{\mathrm{2}} =\mathrm{2}\frac{{t}_{\mathrm{3}} }{{c}^{\mathrm{2}} } \\ $$$$\frac{{s}_{\mathrm{2}} }{{c}_{\mathrm{2}} }+\frac{{s}_{\mathrm{4}} }{{c}_{\mathrm{4}} }−\frac{{s}^{\mathrm{2}} {s}_{\mathrm{3}} ^{\mathrm{2}} {s}_{\mathrm{4}} }{{c}^{\mathrm{2}} {c}_{\mathrm{3}} ^{\mathrm{2}} {c}_{\mathrm{4}} }−\frac{{s}^{\mathrm{2}} {s}_{\mathrm{2}} {s}_{\mathrm{3}} ^{\mathrm{2}} }{{c}^{\mathrm{2}} {c}_{\mathrm{2}} {c}_{\mathrm{3}} ^{\mathrm{2}} }=\mathrm{2}\frac{{s}_{\mathrm{3}} }{{c}^{\mathrm{2}} {c}_{\mathrm{3}} } \\ $$$${s}_{\mathrm{2}} {c}^{\mathrm{2}} {c}_{\mathrm{3}} ^{\mathrm{2}} {c}_{\mathrm{4}} +{s}_{\mathrm{4}} {c}^{\mathrm{2}} {c}_{\mathrm{2}} {c}_{\mathrm{3}} ^{\mathrm{2}} −{s}^{\mathrm{2}} {s}_{\mathrm{3}} ^{\mathrm{2}} {s}_{\mathrm{4}} {c}_{\mathrm{2}} −{s}^{\mathrm{2}} {s}_{\mathrm{2}} {s}_{\mathrm{3}} ^{\mathrm{2}} {c}_{\mathrm{4}} =\mathrm{2}{s}_{\mathrm{3}} {c}_{\mathrm{2}} {c}_{\mathrm{3}} {c}_{\mathrm{4}} \\ $$$$\left({c}^{\mathrm{2}} {c}_{\mathrm{3}} ^{\mathrm{2}} −{s}^{\mathrm{2}} {s}_{\mathrm{3}} ^{\mathrm{2}} \right)\left({s}_{\mathrm{2}} {c}_{\mathrm{4}} +{s}_{\mathrm{4}} {c}_{\mathrm{2}} \right)=\mathrm{2}{s}_{\mathrm{3}} {c}_{\mathrm{2}} {c}_{\mathrm{3}} {c}_{\mathrm{4}} \\ $$$$\left({c}^{\mathrm{2}} {c}_{\mathrm{3}} ^{\mathrm{2}} −\left(\mathrm{1}−{c}^{\mathrm{2}} \right)\left(\mathrm{1}−{c}_{\mathrm{3}} ^{\mathrm{2}} \right)\right)\left({s}_{\mathrm{2}} {c}_{\mathrm{4}} +{s}_{\mathrm{4}} {c}_{\mathrm{2}} \right)=\mathrm{2}{s}_{\mathrm{3}} {c}_{\mathrm{2}} {c}_{\mathrm{3}} {c}_{\mathrm{4}} \\ $$$$\left({c}^{\mathrm{2}} +{c}_{\mathrm{3}} ^{\mathrm{2}} −\mathrm{1}\right)\left({s}_{\mathrm{2}} {c}_{\mathrm{4}} +{s}_{\mathrm{4}} {c}_{\mathrm{2}} \right)=\mathrm{2}{s}_{\mathrm{3}} {c}_{\mathrm{2}} {c}_{\mathrm{3}} {c}_{\mathrm{4}} \\ $$$$\mathrm{now}\:\mathrm{use}\:\mathrm{trigonometric}\:\mathrm{formulas}\:\mathrm{until}\:\mathrm{you} \\ $$$$\mathrm{reach}\:\mathrm{this}... \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}\left({c}_{\mathrm{2}} +{c}_{\mathrm{6}} \right)\right)\left({s}_{\mathrm{6}} \right)=\frac{\mathrm{1}}{\mathrm{4}}\left({s}_{\mathrm{4}} +{s}_{\mathrm{8}} +{s}_{\mathrm{12}} \right) \\ $$$$...\mathrm{and}\:\mathrm{again}: \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left({s}_{\mathrm{4}} +{s}_{\mathrm{8}} +{s}_{\mathrm{12}} \right)=\frac{\mathrm{1}}{\mathrm{4}}\left({s}_{\mathrm{4}} +{s}_{\mathrm{8}} +{s}_{\mathrm{12}} \right) \\ $$

Answered by MJS last updated on 05/Jul/18

t=arctan α tan α → t tan 2α → ((2t)/((1−t)(1+t))) tan 3α → ((t(3−t^2 ))/(1−3t^2 )) tan 4α → ((4t(1−t)(1+t))/((1+2t−t^2 )(1−2t−t^2 ))) sec^2 α → 1+t^2 left side (((2t)/((1−t)(1+t)))+((4t(1−t)(1+t))/((1+2t−t^2 )(1−2t−t^2 ))))= =((2t(1−3t^2 )(3−t^2 ))/((1+2t−t^2 )(1−2t−t^2 )(1−t)(1+t)))=A (1−(((t(3−t^2 ))/(1−3t^2 )))^2 t^2 )=(((1−6t^2 +t^4 )(1+t^2 )(1−t)(1+t))/((1−3t^2 )^2 ))=B A×B=((2t(3−t^2 )(1+t^2 ))/(1−3t^2 )) right side 2((t(3−t^2 ))/(1−3t^2 ))(1+t^2 )

$${t}=\mathrm{arctan}\:\alpha \\ $$$$\mathrm{tan}\:\alpha\:\rightarrow\:{t} \\ $$$$\mathrm{tan}\:\mathrm{2}\alpha\:\rightarrow\:\frac{\mathrm{2}{t}}{\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}\right)} \\ $$$$\mathrm{tan}\:\mathrm{3}\alpha\:\rightarrow\:\frac{{t}\left(\mathrm{3}−{t}^{\mathrm{2}} \right)}{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} } \\ $$$$\mathrm{tan}\:\mathrm{4}\alpha\:\rightarrow\:\frac{\mathrm{4}{t}\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}\right)}{\left(\mathrm{1}+\mathrm{2}{t}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{2}{t}−{t}^{\mathrm{2}} \right)} \\ $$$$\mathrm{sec}^{\mathrm{2}} \:\alpha\:\rightarrow\:\mathrm{1}+{t}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{left}\:\mathrm{side} \\ $$$$\left(\frac{\mathrm{2}{t}}{\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}\right)}+\frac{\mathrm{4}{t}\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}\right)}{\left(\mathrm{1}+\mathrm{2}{t}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{2}{t}−{t}^{\mathrm{2}} \right)}\right)= \\ $$$$=\frac{\mathrm{2}{t}\left(\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} \right)\left(\mathrm{3}−{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{2}{t}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{2}{t}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}\right)}={A} \\ $$$$\left(\mathrm{1}−\left(\frac{{t}\left(\mathrm{3}−{t}^{\mathrm{2}} \right)}{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }\right)^{\mathrm{2}} {t}^{\mathrm{2}} \right)=\frac{\left(\mathrm{1}−\mathrm{6}{t}^{\mathrm{2}} +{t}^{\mathrm{4}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}\right)}{\left(\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} \right)^{\mathrm{2}} }={B} \\ $$$${A}×{B}=\frac{\mathrm{2}{t}\left(\mathrm{3}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} } \\ $$$$ \\ $$$$\mathrm{right}\:\mathrm{side} \\ $$$$\mathrm{2}\frac{{t}\left(\mathrm{3}−{t}^{\mathrm{2}} \right)}{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }\left(\mathrm{1}+{t}^{\mathrm{2}} \right) \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 05/Jul/18

(((sin4α)/(cos4α))+((sin2α)/(cos2α)))(((cos^2 3αcos^2 α−sin^2 3αsin^2 α)/(cos^2 3αcos^2 α))) (((sin6α)/(cos4αcos2α)))(((((1+c6α)/2).((1+c2α)/2)−((1−c6α)/2).((1−c2α)/2))/(c^2 3α.c^2 α))) ((2s3αc3α)/(c4αc2α)).(1/4).((2c6α+2c2α)/(cos^2 3αcos^2 α)) ((sin3αcos3α)/(cos4αcos2α)).((cos6α+cos2α)/(cos^2 3αcos^2 α)) ((sin3αcos3α)/(cos4αcos2α)).2((cos4αcos2α)/(cos^2 3αcos^2 α)) 2tan3αsec^2 α

$$\left(\frac{{sin}\mathrm{4}\alpha}{{cos}\mathrm{4}\alpha}+\frac{{sin}\mathrm{2}\alpha}{{cos}\mathrm{2}\alpha}\right)\left(\frac{{cos}^{\mathrm{2}} \mathrm{3}\alpha{cos}^{\mathrm{2}} \alpha−{sin}^{\mathrm{2}} \mathrm{3}\alpha{sin}^{\mathrm{2}} \alpha}{{cos}^{\mathrm{2}} \mathrm{3}\alpha{cos}^{\mathrm{2}} \alpha}\right) \\ $$$$\left(\frac{{sin}\mathrm{6}\alpha}{{cos}\mathrm{4}\alpha{cos}\mathrm{2}\alpha}\right)\left(\frac{\frac{\mathrm{1}+{c}\mathrm{6}\alpha}{\mathrm{2}}.\frac{\mathrm{1}+{c}\mathrm{2}\alpha}{\mathrm{2}}−\frac{\mathrm{1}−{c}\mathrm{6}\alpha}{\mathrm{2}}.\frac{\mathrm{1}−{c}\mathrm{2}\alpha}{\mathrm{2}}}{{c}^{\mathrm{2}} \mathrm{3}\alpha.{c}^{\mathrm{2}} \alpha}\right) \\ $$$$ \\ $$$$\frac{\mathrm{2}{s}\mathrm{3}\alpha{c}\mathrm{3}\alpha}{{c}\mathrm{4}\alpha{c}\mathrm{2}\alpha}.\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{2}{c}\mathrm{6}\alpha+\mathrm{2}{c}\mathrm{2}\alpha}{{cos}^{\mathrm{2}} \mathrm{3}\alpha{cos}^{\mathrm{2}} \alpha} \\ $$$$\frac{{sin}\mathrm{3}\alpha{cos}\mathrm{3}\alpha}{{cos}\mathrm{4}\alpha{cos}\mathrm{2}\alpha}.\frac{{cos}\mathrm{6}\alpha+{cos}\mathrm{2}\alpha}{{cos}^{\mathrm{2}} \mathrm{3}\alpha{cos}^{\mathrm{2}} \alpha} \\ $$$$\frac{{sin}\mathrm{3}\alpha{cos}\mathrm{3}\alpha}{{cos}\mathrm{4}\alpha{cos}\mathrm{2}\alpha}.\mathrm{2}\frac{{cos}\mathrm{4}\alpha{cos}\mathrm{2}\alpha}{{cos}^{\mathrm{2}} \mathrm{3}\alpha{cos}^{\mathrm{2}} \alpha} \\ $$$$\mathrm{2}{tan}\mathrm{3}\alpha{sec}^{\mathrm{2}} \alpha \\ $$$$\:\:\:\:\: \\ $$

Answered by math1967 last updated on 05/Jul/18

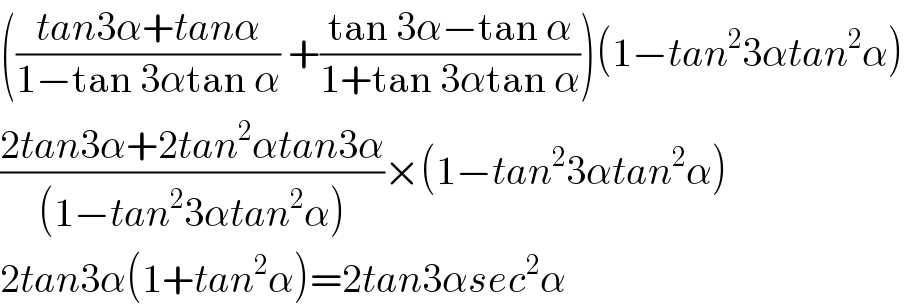
(((tan3α+tanα)/(1−tan 3αtan α)) +((tan 3α−tan α)/(1+tan 3αtan α)))(1−tan^2 3αtan^2 α) ((2tan3α+2tan^2 αtan3α)/((1−tan^2 3αtan^2 α)))×(1−tan^2 3αtan^2 α) 2tan3α(1+tan^2 α)=2tan3αsec^2 α

$$\left(\frac{{tan}\mathrm{3}\alpha+{tan}\alpha}{\mathrm{1}−\mathrm{tan}\:\mathrm{3}\alpha\mathrm{tan}\:\alpha}\:+\frac{\mathrm{tan}\:\mathrm{3}\alpha−\mathrm{tan}\:\alpha}{\mathrm{1}+\mathrm{tan}\:\mathrm{3}\alpha\mathrm{tan}\:\alpha}\right)\left(\mathrm{1}−{tan}^{\mathrm{2}} \mathrm{3}\alpha{tan}^{\mathrm{2}} \alpha\right) \\ $$$$\frac{\mathrm{2}{tan}\mathrm{3}\alpha+\mathrm{2}{tan}^{\mathrm{2}} \alpha{tan}\mathrm{3}\alpha}{\left(\mathrm{1}−{tan}^{\mathrm{2}} \mathrm{3}\alpha{tan}^{\mathrm{2}} \alpha\right)}×\left(\mathrm{1}−{tan}^{\mathrm{2}} \mathrm{3}\alpha{tan}^{\mathrm{2}} \alpha\right) \\ $$$$\mathrm{2}{tan}\mathrm{3}\alpha\left(\mathrm{1}+{tan}^{\mathrm{2}} \alpha\right)=\mathrm{2}{tan}\mathrm{3}\alpha{sec}^{\mathrm{2}} \alpha \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com