
Question Number 83430 by jagoll last updated on 02/Mar/20
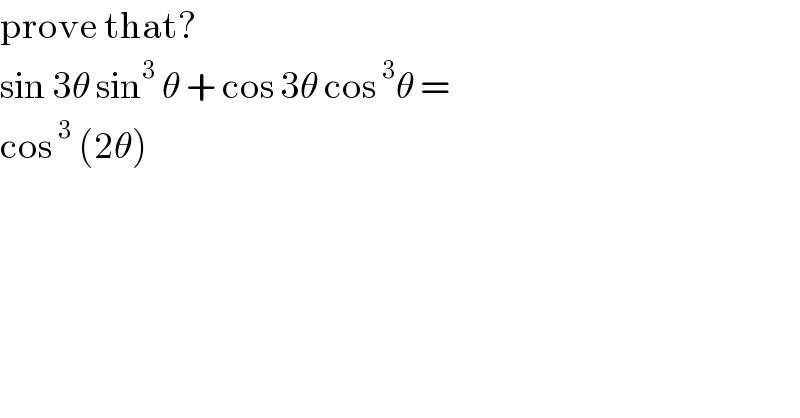
$$\mathrm{prove}\:\mathrm{that}? \\ $$$$\mathrm{sin}\:\mathrm{3}\theta\:\mathrm{sin}^{\mathrm{3}} \:\theta\:+\:\mathrm{cos}\:\mathrm{3}\theta\:\mathrm{cos}\:^{\mathrm{3}} \theta\:=\:\: \\ $$$$\mathrm{cos}\:^{\mathrm{3}} \:\left(\mathrm{2}\theta\right) \\ $$
Answered by mind is power last updated on 02/Mar/20
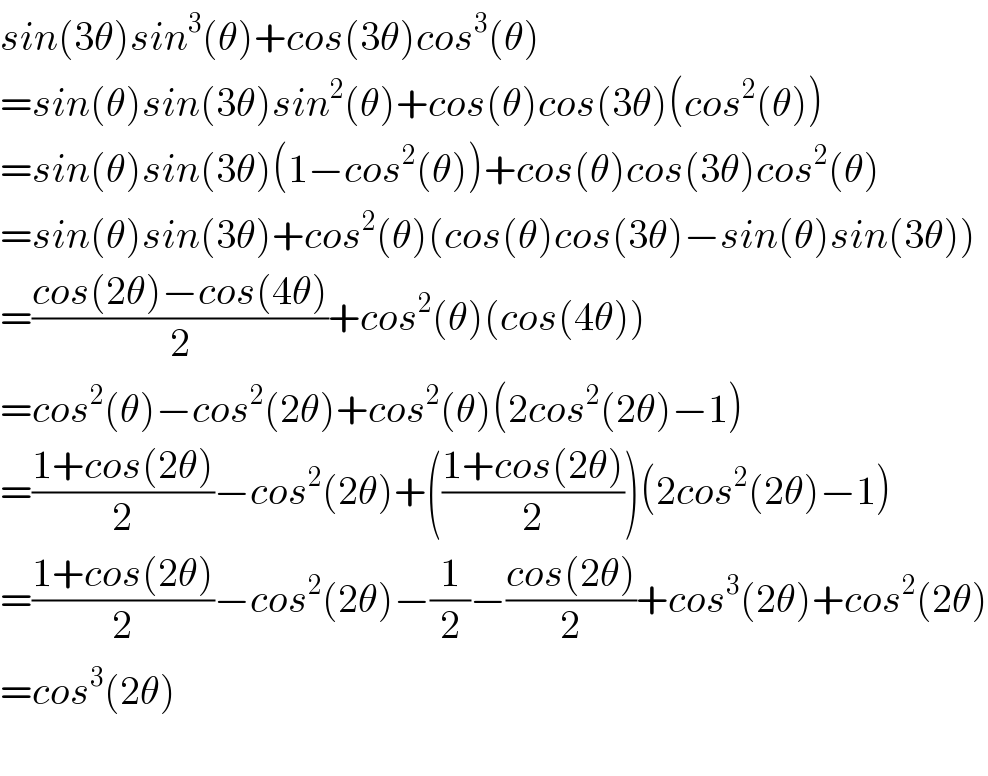
$${sin}\left(\mathrm{3}\theta\right){sin}^{\mathrm{3}} \left(\theta\right)+{cos}\left(\mathrm{3}\theta\right){cos}^{\mathrm{3}} \left(\theta\right) \\ $$$$={sin}\left(\theta\right){sin}\left(\mathrm{3}\theta\right){sin}^{\mathrm{2}} \left(\theta\right)+{cos}\left(\theta\right){cos}\left(\mathrm{3}\theta\right)\left({cos}^{\mathrm{2}} \left(\theta\right)\right) \\ $$$$={sin}\left(\theta\right){sin}\left(\mathrm{3}\theta\right)\left(\mathrm{1}−{cos}^{\mathrm{2}} \left(\theta\right)\right)+{cos}\left(\theta\right){cos}\left(\mathrm{3}\theta\right){cos}^{\mathrm{2}} \left(\theta\right) \\ $$$$={sin}\left(\theta\right){sin}\left(\mathrm{3}\theta\right)+{cos}^{\mathrm{2}} \left(\theta\right)\left({cos}\left(\theta\right){cos}\left(\mathrm{3}\theta\right)−{sin}\left(\theta\right){sin}\left(\mathrm{3}\theta\right)\right) \\ $$$$=\frac{{cos}\left(\mathrm{2}\theta\right)−{cos}\left(\mathrm{4}\theta\right)}{\mathrm{2}}+{cos}^{\mathrm{2}} \left(\theta\right)\left({cos}\left(\mathrm{4}\theta\right)\right) \\ $$$$={cos}^{\mathrm{2}} \left(\theta\right)−{cos}^{\mathrm{2}} \left(\mathrm{2}\theta\right)+{cos}^{\mathrm{2}} \left(\theta\right)\left(\mathrm{2}{cos}^{\mathrm{2}} \left(\mathrm{2}\theta\right)−\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}−{cos}^{\mathrm{2}} \left(\mathrm{2}\theta\right)+\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\right)\left(\mathrm{2}{cos}^{\mathrm{2}} \left(\mathrm{2}\theta\right)−\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}−{cos}^{\mathrm{2}} \left(\mathrm{2}\theta\right)−\frac{\mathrm{1}}{\mathrm{2}}−\frac{{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}+{cos}^{\mathrm{3}} \left(\mathrm{2}\theta\right)+{cos}^{\mathrm{2}} \left(\mathrm{2}\theta\right) \\ $$$$={cos}^{\mathrm{3}} \left(\mathrm{2}\theta\right) \\ $$$$ \\ $$
Commented by mind is power last updated on 02/Mar/20

$${withe}\:{pleasur} \\ $$
Commented by jagoll last updated on 02/Mar/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
