
Question Number 122045 by mohammad17 last updated on 13/Nov/20

$${prove}\:{that}\:\Gamma{s}\:\Gamma\mathrm{1}−{s}=\frac{\pi}{{sins}\pi} \\ $$
Commented by Dwaipayan Shikari last updated on 14/Nov/20
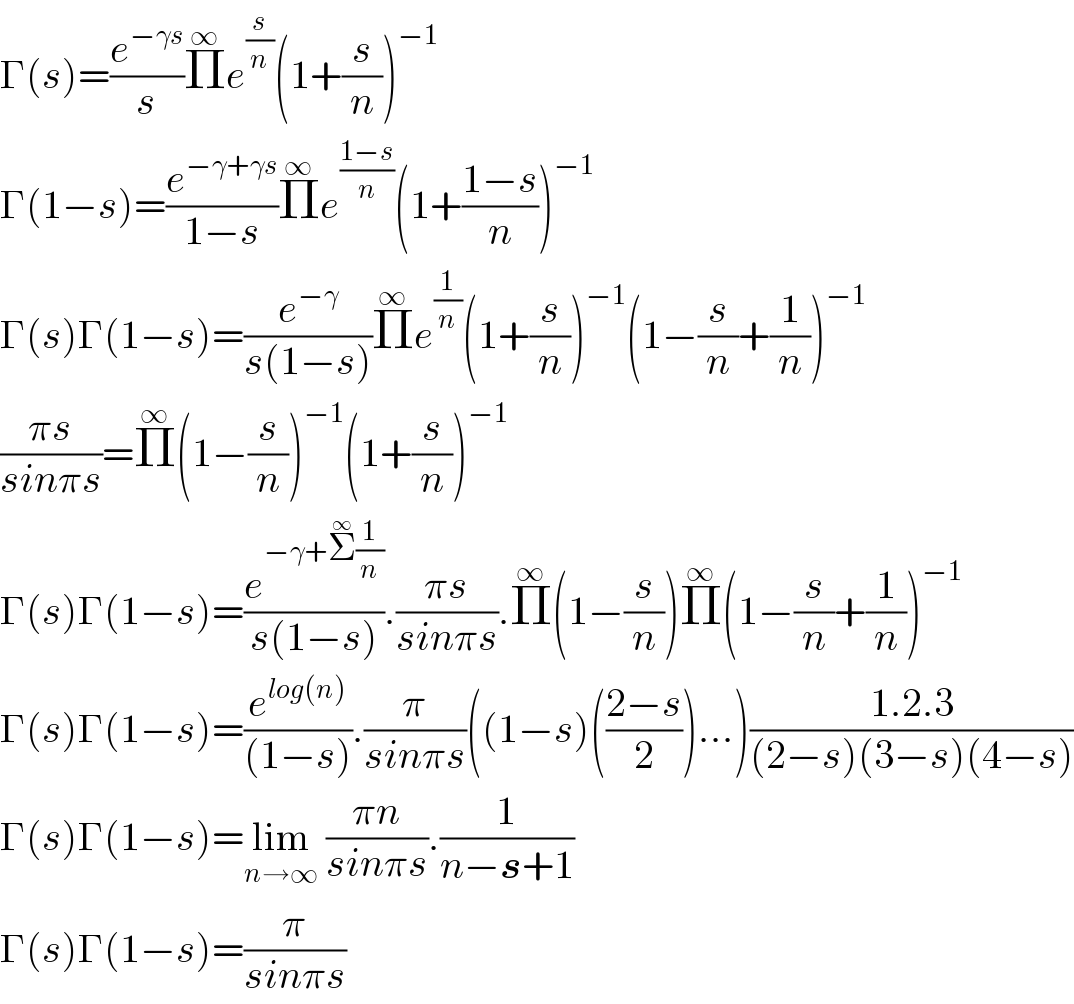
$$\Gamma\left({s}\right)=\frac{{e}^{−\gamma{s}} }{{s}}\overset{\infty} {\prod}{e}^{\frac{{s}}{{n}}} \left(\mathrm{1}+\frac{{s}}{{n}}\right)^{−\mathrm{1}} \\ $$$$\Gamma\left(\mathrm{1}−{s}\right)=\frac{{e}^{−\gamma+\gamma{s}} }{\mathrm{1}−{s}}\overset{\infty} {\prod}{e}^{\frac{\mathrm{1}−{s}}{{n}}} \left(\mathrm{1}+\frac{\mathrm{1}−{s}}{{n}}\right)^{−\mathrm{1}} \\ $$$$\Gamma\left({s}\right)\Gamma\left(\mathrm{1}−{s}\right)=\frac{{e}^{−\gamma} }{{s}\left(\mathrm{1}−{s}\right)}\overset{\infty} {\prod}{e}^{\frac{\mathrm{1}}{{n}}} \left(\mathrm{1}+\frac{{s}}{{n}}\right)^{−\mathrm{1}} \left(\mathrm{1}−\frac{{s}}{{n}}+\frac{\mathrm{1}}{{n}}\right)^{−\mathrm{1}} \\ $$$$\frac{\pi{s}}{{sin}\pi{s}}=\overset{\infty} {\prod}\left(\mathrm{1}−\frac{{s}}{{n}}\right)^{−\mathrm{1}} \left(\mathrm{1}+\frac{{s}}{{n}}\right)^{−\mathrm{1}} \\ $$$$\Gamma\left({s}\right)\Gamma\left(\mathrm{1}−{s}\right)=\frac{{e}^{−\gamma+\overset{\infty} {\sum}\frac{\mathrm{1}}{{n}}} }{{s}\left(\mathrm{1}−{s}\right)}.\frac{\pi{s}}{{sin}\pi{s}}.\overset{\infty} {\prod}\left(\mathrm{1}−\frac{{s}}{{n}}\right)\overset{\infty} {\prod}\left(\mathrm{1}−\frac{{s}}{{n}}+\frac{\mathrm{1}}{{n}}\right)^{−\mathrm{1}} \\ $$$$\Gamma\left({s}\right)\Gamma\left(\mathrm{1}−{s}\right)=\frac{{e}^{{log}\left({n}\right)} }{\left(\mathrm{1}−{s}\right)}.\frac{\pi}{{sin}\pi{s}}\left(\left(\mathrm{1}−{s}\right)\left(\frac{\mathrm{2}−{s}}{\mathrm{2}}\right)...\right)\frac{\mathrm{1}.\mathrm{2}.\mathrm{3}}{\left(\mathrm{2}−{s}\right)\left(\mathrm{3}−{s}\right)\left(\mathrm{4}−{s}\right)} \\ $$$$\Gamma\left({s}\right)\Gamma\left(\mathrm{1}−{s}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\pi{n}}{{sin}\pi{s}}.\frac{\mathrm{1}}{{n}−\boldsymbol{{s}}+\mathrm{1}} \\ $$$$\Gamma\left({s}\right)\Gamma\left(\mathrm{1}−{s}\right)=\frac{\pi}{{sin}\pi{s}} \\ $$
Commented by mnjuly1970 last updated on 14/Nov/20

$${bravo}\:{mr}\:{dwaipayan}.. \\ $$$${very}\:{nice}\:{as}\:{always}... \\ $$
Commented by Dwaipayan Shikari last updated on 14/Nov/20
With pleasure��
Answered by mnjuly1970 last updated on 14/Nov/20

$$\:{proof}\:{by}\:{using}\:{double} \\ $$$$\:\:{integral}. \\ $$$$\:\:\Gamma\left({s}\right)=\int_{\mathrm{0}} ^{\:\infty} {x}^{{s}−\mathrm{1}} {e}^{−{x}} {dx}\:...\left({i}\right) \\ $$$$\:\:\:\Gamma\left(\mathrm{1}−{s}\right)=\int_{\mathrm{0}} ^{\:\infty} {y}^{−{s}} {e}^{−{y}} {dy}...\left({ii}\right) \\ $$$$\:{from}\:\:\left({i}\right)\:{and}\:\left({ii}\right): \\ $$$$\:\:\Gamma\left({s}\right)\Gamma\left(\mathrm{1}−{s}\right)=\int_{\mathrm{0}} ^{\:\infty} \int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}}{{x}}\left(\frac{{x}}{{y}}\right)^{{s}} {e}^{−\left({x}+{y}\right)} {dx}\:{dy} \\ $$$$\:\:\:\left\{_{\frac{{x}}{{y}}={v}} ^{{x}+{y}={u}} \:\Rightarrow\left\{_{{x}=\frac{{uv}}{\mathrm{1}+{v}}} ^{{y}=\frac{{u}}{\mathrm{1}+{v}}} \right.\right. \\ $$$$\:\:\:\:{dxdy}=\mid\frac{\partial\left({x},{y}\right)}{\partial\left({u},{v}\right)}\mid{dudv}\:\:{where} \\ $$$$\:\:\:\:\:\:\frac{\partial\left({x},{y}\right)}{\partial\left({u},{v}\right)}={J}\left({u},{v}\right)=\begin{vmatrix}{\frac{\partial{x}}{\partial{u}}\:\:\:\:\:\:\:\:\:\:\frac{\partial{x}}{\partial{v}}}\\{\frac{\partial{y}}{\partial{u}}\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\partial{y}}{\partial{v}}\:}\end{vmatrix} \\ $$$$\:\:\:\:\therefore\:\:{J}\left({u},{v}\right)={x}_{{u}} {y}_{{v}} −{x}_{{v}} {y}_{{u}} =\left(\frac{{v}}{\mathrm{1}+{v}}\right)\left(\frac{−{u}}{\left(\mathrm{1}+{v}\right)^{\mathrm{2}} }\right)−\left(\frac{{u}}{\left(\mathrm{1}+{v}\right)^{\mathrm{2}} }\right)\left(\frac{\mathrm{1}}{\mathrm{1}+{v}}\right) \\ $$$$\:\:\:\:\:\:\:{J}\left({u},{v}\right)=\frac{−{u}}{\left(\mathrm{1}+{v}\right)^{\mathrm{2}} }\:\checkmark \\ $$$$\:\:\:\:\:\Gamma\left({s}\right)\Gamma\left(\mathrm{1}−{s}\right)=\int_{\mathrm{0}} ^{\:\infty} \int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}+{v}}{{uv}}{v}^{{s}} {e}^{−{u}} \mid\frac{−{u}}{\left(\mathrm{1}+{v}\right)^{\mathrm{2}} }\mid{dudv} \\ $$$$=\int_{\mathrm{0}} ^{\:\infty} \int_{\mathrm{0}} ^{\:\infty} \frac{{v}^{{s}−\mathrm{1}} }{\mathrm{1}+{v}}{e}^{−{u}} {dudv}=\int_{\mathrm{0}} ^{\:\infty} \frac{{v}^{{s}−\mathrm{1}} }{\mathrm{1}+{v}}{dv}\underset{{analysis}} {\overset{{complex}} {=}}\frac{\pi}{{sin}\left(\pi{s}\right)}\:\checkmark \\ $$$$\:\:\:\:\:\:\:...{m}.{n}... \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 14/Nov/20

$${Great}! \\ $$
Commented by mnjuly1970 last updated on 14/Nov/20

$${thank}\:{you}.. \\ $$$$ \\ $$
