
Question Number 50914 by peter frank last updated on 22/Dec/18
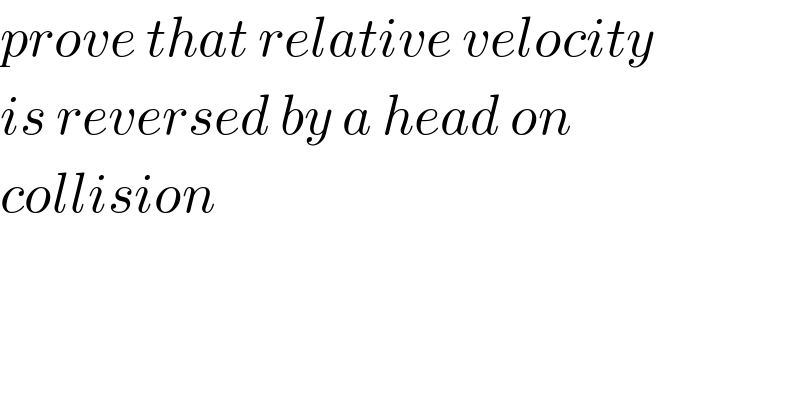
$${prove}\:{that}\:{relative}\:{velocity} \\ $$$${is}\:{reversed}\:{by}\:{a}\:{head}\:{on} \\ $$$${collision} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Dec/18
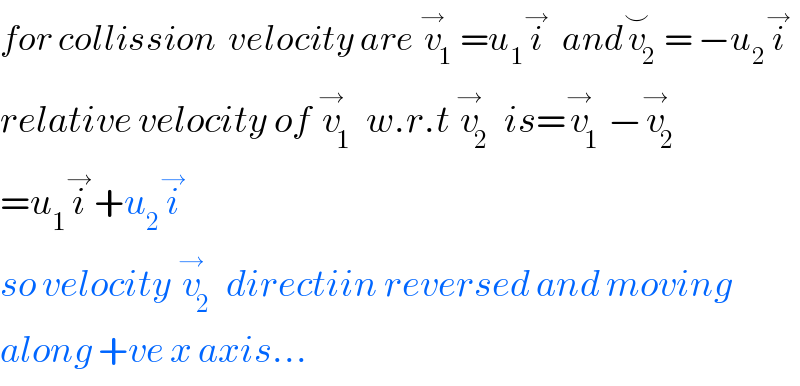
$${for}\:{collission}\:\:{velocity}\:{are}\:\overset{\rightarrow} {{v}}_{\mathrm{1}} ={u}_{\mathrm{1}} \overset{\rightarrow} {{i}}\:\:{and}\overset{\smile} {{v}}_{\mathrm{2}} =\:−{u}_{\mathrm{2}} \overset{\rightarrow} {{i}} \\ $$$${relative}\:{velocity}\:{of}\:\overset{\rightarrow} {{v}}_{\mathrm{1}} \:{w}.{r}.{t}\:\overset{\rightarrow} {{v}}_{\mathrm{2}} \:{is}=\overset{\rightarrow} {{v}}_{\mathrm{1}} −\overset{\rightarrow} {{v}}_{\mathrm{2}} \\ $$$$={u}_{\mathrm{1}} \overset{\rightarrow} {{i}}+{u}_{\mathrm{2}} \overset{\rightarrow} {{i}} \\ $$$${so}\:{velocity}\:\overset{\rightarrow} {{v}}_{\mathrm{2}} \:{directiin}\:{reversed}\:{and}\:{moving} \\ $$$${along}\:+{ve}\:{x}\:{axis}... \\ $$
Commented by peter frank last updated on 22/Dec/18

$${thank}\:{you} \\ $$
Answered by peter frank last updated on 22/Dec/18
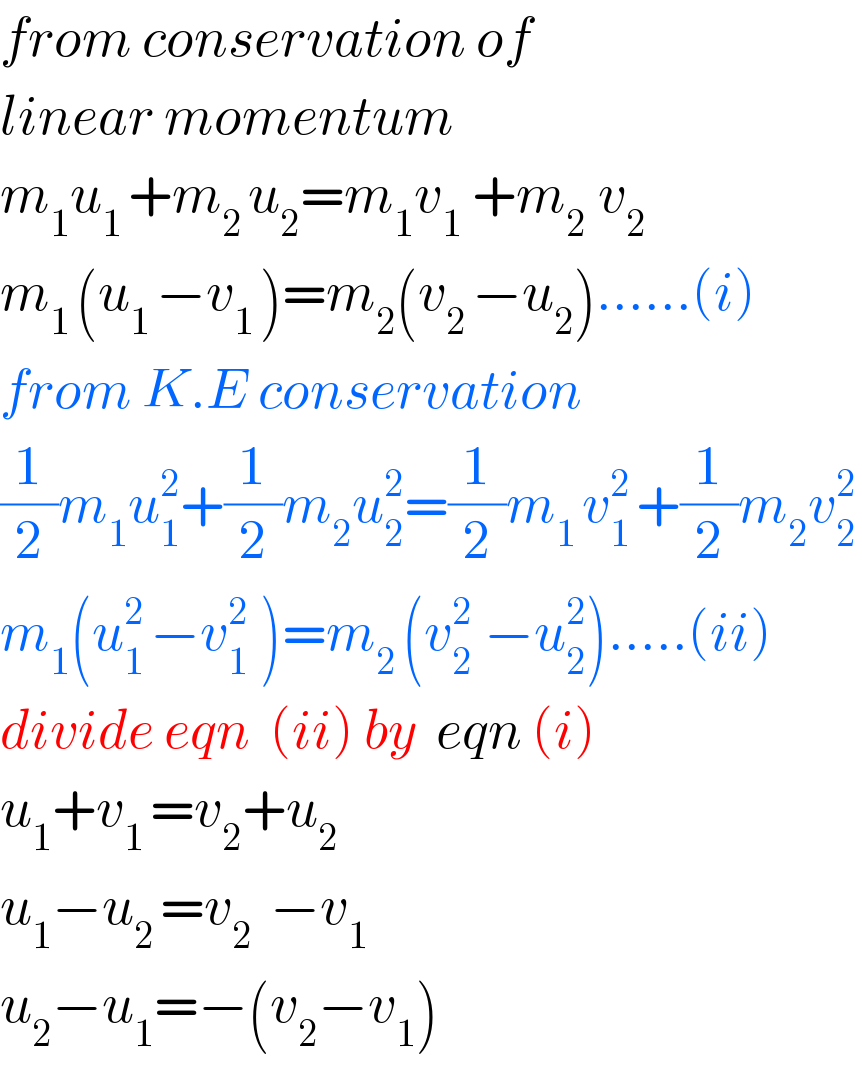
$${from}\:{conservation}\:{of}\: \\ $$$${linear}\:{momentum} \\ $$$${m}_{\mathrm{1}} {u}_{\mathrm{1}\:} +{m}_{\mathrm{2}\:} {u}_{\mathrm{2}} ={m}_{\mathrm{1}} {v}_{\mathrm{1}} \:+{m}_{\mathrm{2}\:\:} {v}_{\mathrm{2}} \\ $$$${m}_{\mathrm{1}\:} \left({u}_{\mathrm{1}\:} −{v}_{\mathrm{1}\:} \right)={m}_{\mathrm{2}} \left({v}_{\mathrm{2}\:} −{u}_{\mathrm{2}} \right)......\left({i}\right) \\ $$$${from}\:{K}.{E}\:{conservation} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{m}_{\mathrm{1}} {u}_{\mathrm{1}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{m}_{\mathrm{2}} {u}_{\mathrm{2}} ^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}{m}_{\mathrm{1}\:} {v}_{\mathrm{1}\:} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{m}_{\mathrm{2}} {v}_{\mathrm{2}\:} ^{\mathrm{2}} \\ $$$${m}_{\mathrm{1}} \left({u}_{\mathrm{1}\:} ^{\mathrm{2}} −{v}_{\mathrm{1}\:\:} ^{\mathrm{2}} \right)={m}_{\mathrm{2}\:} \left({v}_{\mathrm{2}\:\:} ^{\mathrm{2}} −{u}_{\mathrm{2}} ^{\mathrm{2}} \right).....\left({ii}\right) \\ $$$${divide}\:{eqn}\:\:\left({ii}\right)\:{by}\:\:{eqn}\:\left({i}\right) \\ $$$${u}_{\mathrm{1}} +{v}_{\mathrm{1}\:} ={v}_{\mathrm{2}} +{u}_{\mathrm{2}} \\ $$$${u}_{\mathrm{1}} −{u}_{\mathrm{2}\:} ={v}_{\mathrm{2}\:\:\:} −{v}_{\mathrm{1}} \\ $$$${u}_{\mathrm{2}} −{u}_{\mathrm{1}} =−\left({v}_{\mathrm{2}} −{v}_{\mathrm{1}} \right) \\ $$
