
Question Number 76367 by Rio Michael last updated on 26/Dec/19
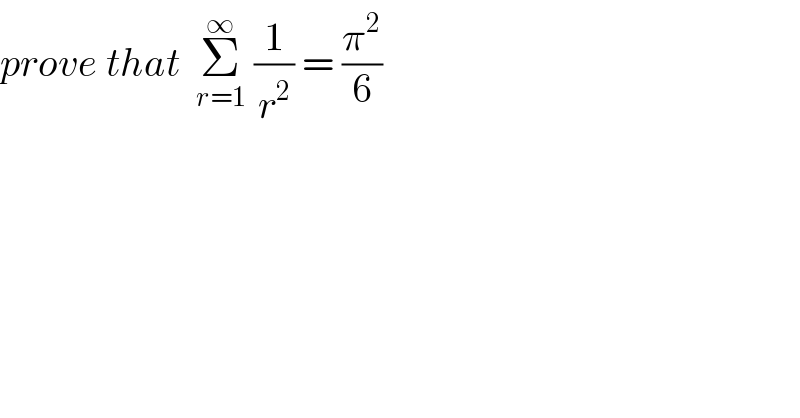
$${prove}\:{that}\:\:\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$
Commented by mathmax by abdo last updated on 26/Dec/19

$${not}\:{correct} \\ $$
Commented by mathmax by abdo last updated on 26/Dec/19

$${i}\:{think}\:\sum_{{r}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{r}^{\mathrm{2}} } \\ $$
Commented by Rio Michael last updated on 26/Dec/19
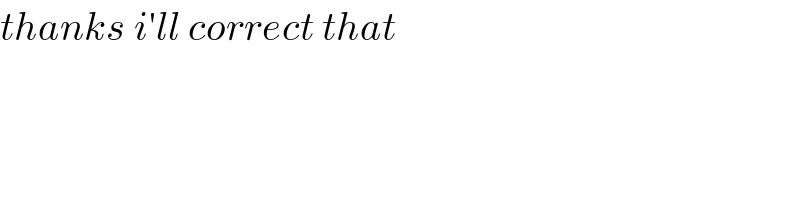
$${thanks}\:{i}'{ll}\:{correct}\:{that} \\ $$
Commented by mathmax by abdo last updated on 28/Dec/19
![let f(x)=∣x∣ ,2π periodic even f(x) =(a_0 /2) +Σ_(n=1) ^∞ a_n cos(nx) a_n =(2/T)∫_([T]) ∣x∣ cos(nx) =(1/π)∫_(−π) ^π ∣x∣ cos(nx)dx =(2/π) ∫_0 ^π x cos(nx)dx ⇒(π/2)a_n =∫_0 ^π x cos(nx) =_(by parts) [(x/n)sin(nx)]_0 ^π −∫_0 ^π (1/n)sin(nx)dx =−(1/n)[−(1/n)cos(nx)]_0 ^π =(1/n^2 ){(−1)^n −1) ⇒ a_n =(2/(πn^2 )){ (−1)^n −1} a_0 =(2/π)×(π^2 /2)=π ⇒∣x∣ =(π/2) +(2/π)Σ_(n=1) ^∞ (((−1)^n −1)/n^2 )cos(nx) =(π/2) +(2/π)(−2) Σ_(p=0) ^∞ (1/((2p+1)^2 ))cos(2p+1)x =(π/2)−(4/π) Σ_(p=0) ^∞ ((cos(2p+1)x)/((2p+1)^2 )) x=0 ⇒(π/2)−(4/π) Σ_(p=0) ^∞ (1/((2p+1)^2 )) =0 ⇒(4/π)Σ_(p=0) ^∞ (1/((2p+1)^2 )) =(π/2) ⇒ Σ_(p=0) ^∞ (1/((2p+1)^2 )) =(π^2 /8) Σ_(n=1) ^∞ (1/n^2 ) =Σ_(n=1) ^∞ (1/(4n^2 )) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ (3/4) Σ_(n=1) ^∞ (1/n^2 ) =(π^2 /8) ⇒ Σ_(n=1) ^∞ (1/n^2 ) =(4/3)×(π^2 /8) =(π^2 /6) .](Q76611.png)
$${let}\:{f}\left({x}\right)=\mid{x}\mid\:,\mathrm{2}\pi\:{periodic}\:{even} \\ $$$${f}\left({x}\right)\:=\frac{{a}_{\mathrm{0}} }{\mathrm{2}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:{a}_{{n}} {cos}\left({nx}\right) \\ $$$${a}_{{n}} =\frac{\mathrm{2}}{{T}}\int_{\left[{T}\right]} \mid{x}\mid\:{cos}\left({nx}\right)\:=\frac{\mathrm{1}}{\pi}\int_{−\pi} ^{\pi} \:\mid{x}\mid\:{cos}\left({nx}\right){dx} \\ $$$$=\frac{\mathrm{2}}{\pi}\:\int_{\mathrm{0}} ^{\pi} \:{x}\:{cos}\left({nx}\right){dx}\:\Rightarrow\frac{\pi}{\mathrm{2}}{a}_{{n}} =\int_{\mathrm{0}} ^{\pi} \:{x}\:{cos}\left({nx}\right) \\ $$$$=_{{by}\:{parts}} \:\:\left[\frac{{x}}{{n}}{sin}\left({nx}\right)\right]_{\mathrm{0}} ^{\pi} \:−\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}}{{n}}{sin}\left({nx}\right){dx} \\ $$$$=−\frac{\mathrm{1}}{{n}}\left[−\frac{\mathrm{1}}{{n}}{cos}\left({nx}\right)\right]_{\mathrm{0}} ^{\pi} \:=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left\{\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}\right)\:\Rightarrow \\ $$$${a}_{{n}} =\frac{\mathrm{2}}{\pi{n}^{\mathrm{2}} }\left\{\:\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}\right\} \\ $$$${a}_{\mathrm{0}} =\frac{\mathrm{2}}{\pi}×\frac{\pi^{\mathrm{2}} }{\mathrm{2}}=\pi\:\Rightarrow\mid{x}\mid\:=\frac{\pi}{\mathrm{2}}\:+\frac{\mathrm{2}}{\pi}\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}}{{n}^{\mathrm{2}} }{cos}\left({nx}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}\:+\frac{\mathrm{2}}{\pi}\left(−\mathrm{2}\right)\:\sum_{{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} }{cos}\left(\mathrm{2}{p}+\mathrm{1}\right){x} \\ $$$$=\frac{\pi}{\mathrm{2}}−\frac{\mathrm{4}}{\pi}\:\sum_{{p}=\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left(\mathrm{2}{p}+\mathrm{1}\right){x}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${x}=\mathrm{0}\:\Rightarrow\frac{\pi}{\mathrm{2}}−\frac{\mathrm{4}}{\pi}\:\sum_{{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{0}\:\Rightarrow\frac{\mathrm{4}}{\pi}\sum_{{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$$\sum_{{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\frac{\mathrm{4}}{\mathrm{3}}×\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:. \\ $$
