
Previous in Relation and Functions Next in Relation and Functions
Question Number 68129 by mathmax by abdo last updated on 05/Sep/19
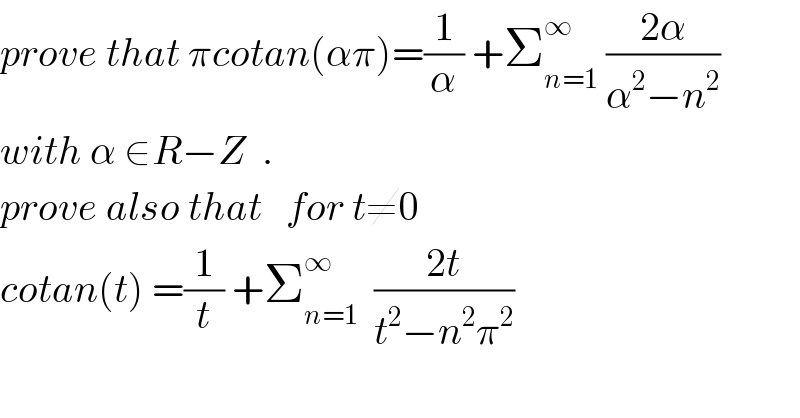
$${prove}\:{that}\:\pi{cotan}\left(\alpha\pi\right)=\frac{\mathrm{1}}{\alpha}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{2}\alpha}{\alpha^{\mathrm{2}} −{n}^{\mathrm{2}} } \\ $$$${with}\:\alpha\:\in{R}−{Z}\:\:. \\ $$$${prove}\:{also}\:{that}\:\:\:{for}\:{t}\neq\mathrm{0} \\ $$$${cotan}\left({t}\right)\:=\frac{\mathrm{1}}{{t}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} −{n}^{\mathrm{2}} \pi^{\mathrm{2}} } \\ $$
