Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 210666 by universe last updated on 15/Aug/24

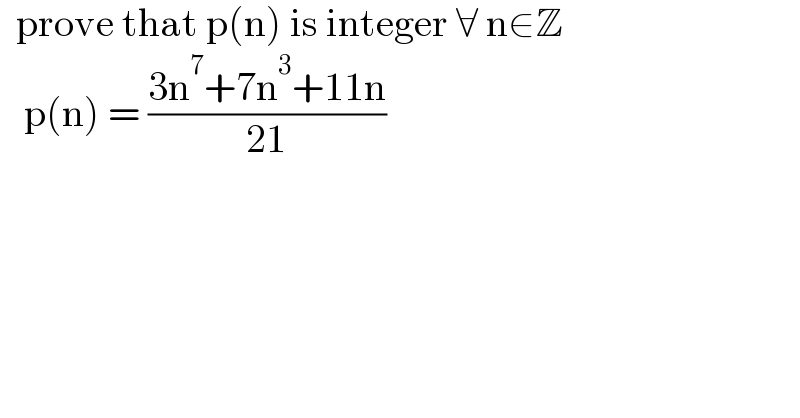
prove that p(n) is integer ∀ n∈Z p(n) = ((3n^7 +7n^3 +11n)/(21))

$$\:\:\mathrm{prove}\:\mathrm{that}\:\mathrm{p}\left(\mathrm{n}\right)\:\mathrm{is}\:\mathrm{integer}\:\forall\:\mathrm{n}\in\mathbb{Z} \\ $$$$\:\:\:\mathrm{p}\left(\mathrm{n}\right)\:=\:\frac{\mathrm{3n}^{\mathrm{7}} +\mathrm{7n}^{\mathrm{3}} +\mathrm{11n}}{\mathrm{21}} \\ $$

Answered by A5T last updated on 15/Aug/24

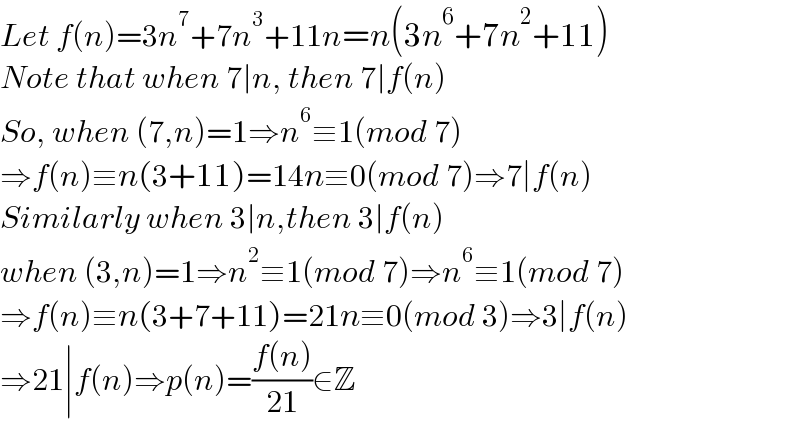
Let f(n)=3n^7 +7n^3 +11n=n(3n^6 +7n^2 +11) Note that when 7∣n, then 7∣f(n) So, when (7,n)=1⇒n^6 ≡1(mod 7) ⇒f(n)≡n(3+11)=14n≡0(mod 7)⇒7∣f(n) Similarly when 3∣n,then 3∣f(n) when (3,n)=1⇒n^2 ≡1(mod 7)⇒n^6 ≡1(mod 7) ⇒f(n)≡n(3+7+11)=21n≡0(mod 3)⇒3∣f(n) ⇒21∣f(n)⇒p(n)=((f(n))/(21))∈Z

$${Let}\:{f}\left({n}\right)=\mathrm{3}{n}^{\mathrm{7}} +\mathrm{7}{n}^{\mathrm{3}} +\mathrm{11}{n}={n}\left(\mathrm{3}{n}^{\mathrm{6}} +\mathrm{7}{n}^{\mathrm{2}} +\mathrm{11}\right) \\ $$$${Note}\:{that}\:{when}\:\mathrm{7}\mid{n},\:{then}\:\mathrm{7}\mid{f}\left({n}\right) \\ $$$${So},\:{when}\:\left(\mathrm{7},{n}\right)=\mathrm{1}\Rightarrow{n}^{\mathrm{6}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right) \\ $$$$\Rightarrow{f}\left({n}\right)\equiv{n}\left(\mathrm{3}+\mathrm{11}\right)=\mathrm{14}{n}\equiv\mathrm{0}\left({mod}\:\mathrm{7}\right)\Rightarrow\mathrm{7}\mid{f}\left({n}\right) \\ $$$${Similarly}\:{when}\:\mathrm{3}\mid{n},{then}\:\mathrm{3}\mid{f}\left({n}\right) \\ $$$${when}\:\left(\mathrm{3},{n}\right)=\mathrm{1}\Rightarrow{n}^{\mathrm{2}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right)\Rightarrow{n}^{\mathrm{6}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right) \\ $$$$\Rightarrow{f}\left({n}\right)\equiv{n}\left(\mathrm{3}+\mathrm{7}+\mathrm{11}\right)=\mathrm{21}{n}\equiv\mathrm{0}\left({mod}\:\mathrm{3}\right)\Rightarrow\mathrm{3}\mid{f}\left({n}\right) \\ $$$$\Rightarrow\mathrm{21}\mid{f}\left({n}\right)\Rightarrow{p}\left({n}\right)=\frac{{f}\left({n}\right)}{\mathrm{21}}\in\mathbb{Z} \\ $$

Commented by universe last updated on 15/Aug/24

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com