
Previous in Relation and Functions Next in Relation and Functions
Question Number 32369 by prof Abdo imad last updated on 23/Mar/18
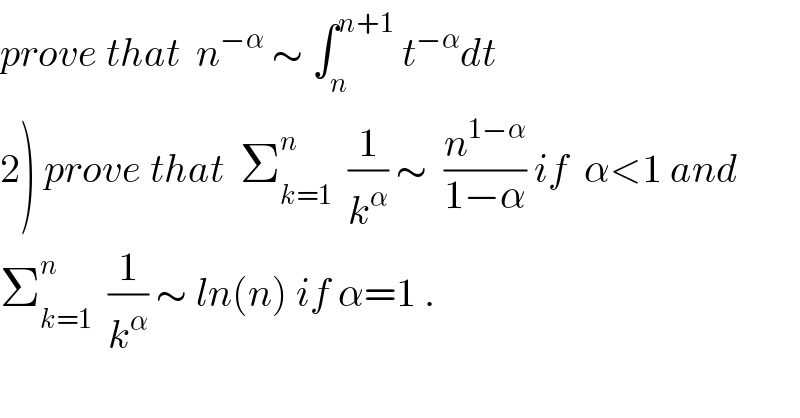
$${prove}\:{that}\:\:{n}^{−\alpha} \:\sim\:\int_{{n}} ^{{n}+\mathrm{1}} \:{t}^{−\alpha} {dt} \\ $$$$\left.\mathrm{2}\right)\:{prove}\:{that}\:\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{{k}^{\alpha} }\:\sim\:\:\frac{{n}^{\mathrm{1}−\alpha} }{\mathrm{1}−\alpha}\:{if}\:\:\alpha<\mathrm{1}\:{and} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{{k}^{\alpha} }\:\sim\:{ln}\left({n}\right)\:{if}\:\alpha=\mathrm{1}\:. \\ $$
