
Previous in Relation and Functions Next in Relation and Functions
Question Number 108688 by abdomsup last updated on 18/Aug/20
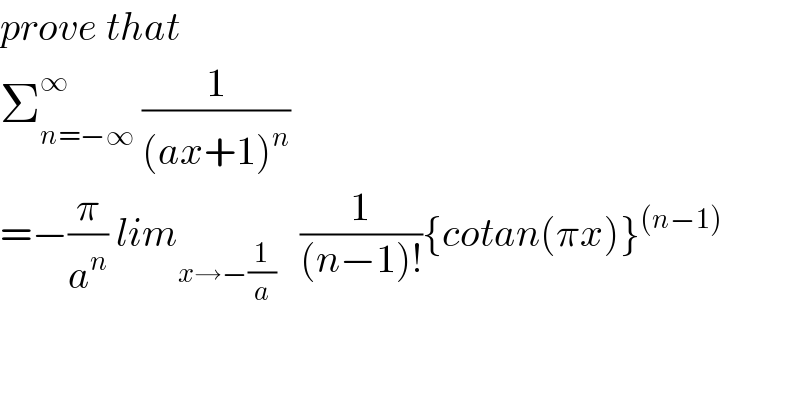
$${prove}\:{that}\: \\ $$$$\sum_{{n}=−\infty} ^{\infty} \:\frac{\mathrm{1}}{\left({ax}+\mathrm{1}\right)^{{n}} } \\ $$$$=−\frac{\pi}{{a}^{{n}} }\:{lim}_{{x}\rightarrow−\frac{\mathrm{1}}{{a}}} \:\:\:\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}\left\{{cotan}\left(\pi{x}\right)\right\}^{\left({n}−\mathrm{1}\right)} \\ $$
Commented by mathdave last updated on 18/Aug/20
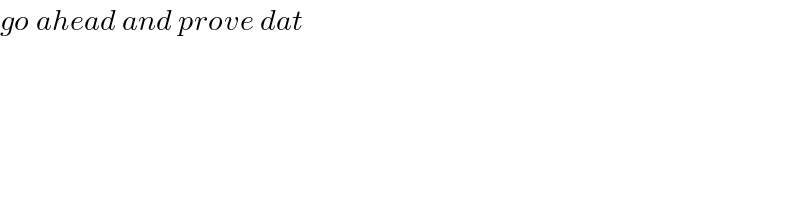
$${go}\:{ahead}\:{and}\:{prove}\:{dat} \\ $$
Commented by mathmax by abdo last updated on 18/Aug/20
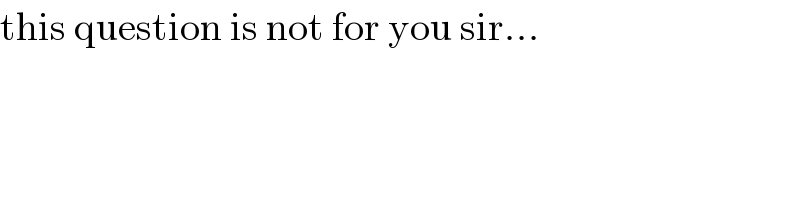
$$\mathrm{this}\:\mathrm{question}\:\mathrm{is}\:\mathrm{not}\:\mathrm{for}\:\mathrm{you}\:\mathrm{sir}... \\ $$
Commented by mathdave last updated on 18/Aug/20
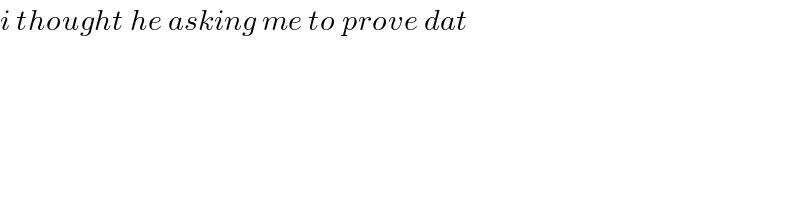
$${i}\:{thought}\:{he}\:{asking}\:{me}\:{to}\:{prove}\:{dat}\: \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 18/Aug/20

$$\mathrm{no}\:\mathrm{sir}... \\ $$
