
Question Number 105625 by M±th+et+s last updated on 30/Jul/20
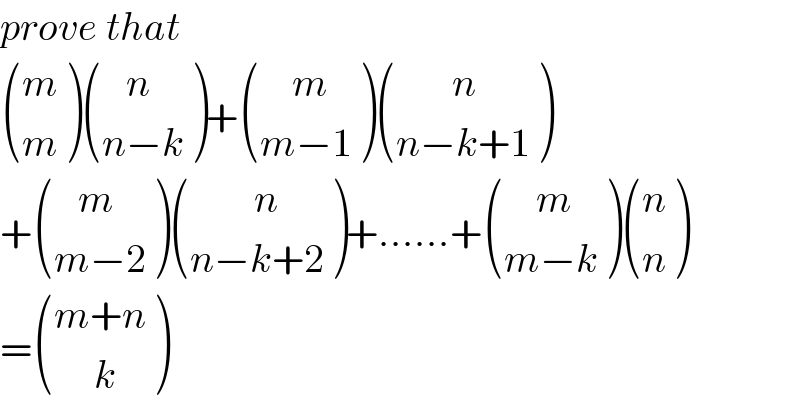
$${prove}\:{that} \\ $$$$\begin{pmatrix}{{m}}\\{{m}}\end{pmatrix}\begin{pmatrix}{\:\:\:{n}}\\{{n}−{k}}\end{pmatrix}+\begin{pmatrix}{\:\:\:\:{m}}\\{{m}−\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\:\:\:\:\:\:\:{n}}\\{{n}−{k}+\mathrm{1}}\end{pmatrix} \\ $$$$+\begin{pmatrix}{\:\:\:{m}}\\{{m}−\mathrm{2}}\end{pmatrix}\begin{pmatrix}{\:\:\:\:\:\:\:\:{n}}\\{{n}−{k}+\mathrm{2}}\end{pmatrix}+......+\begin{pmatrix}{\:\:\:\:{m}}\\{{m}−{k}}\end{pmatrix}\begin{pmatrix}{{n}}\\{{n}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{{m}+{n}}\\{\:\:\:\:\:{k}}\end{pmatrix} \\ $$
Answered by prakash jain last updated on 30/Jul/20

$$\left(\mathrm{1}+{x}\right)^{{m}+{n}} =\left(\mathrm{1}+{x}\right)^{{m}} \left(\mathrm{1}+{x}\right)^{{n}} \\ $$$$\mathrm{compare}\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{{k}} \:\mathrm{on}\:\mathrm{LHS} \\ $$$$\mathrm{and}\:\mathrm{RHS}. \\ $$$$\mathrm{LHS}=\mathrm{C}_{{k}} ^{{m}+{n}} \\ $$$$\mathrm{RHS} \\ $$$$\left({C}_{\mathrm{0}} ^{{m}} {x}^{{m}} +{C}_{\mathrm{1}} ^{{m}} {x}^{{m}−\mathrm{1}} +..+{C}_{{m}−{k}} ^{{m}} {x}^{{k}} +..+{C}_{{m}} ^{{m}} \right)× \\ $$$$\left({C}_{\mathrm{0}} ^{{n}} {x}^{{n}} +{C}_{\mathrm{1}} ^{{n}} {x}^{{n}−\mathrm{1}} +..+{C}_{{n}−{k}} ^{{n}} {x}^{{k}} +..+{C}_{{n}} ^{{n}} \right)× \\ $$$${coefficient}\:{of}\:{x}^{{k}} \\ $$$${C}_{{m}} ^{{m}} {C}_{{n}−{k}} ^{{n}} +..+{C}_{{n}} ^{{n}} {C}_{{n}−{k}} ^{{n}} \\ $$
