
Question Number 40434 by vitlu last updated on 21/Jul/18
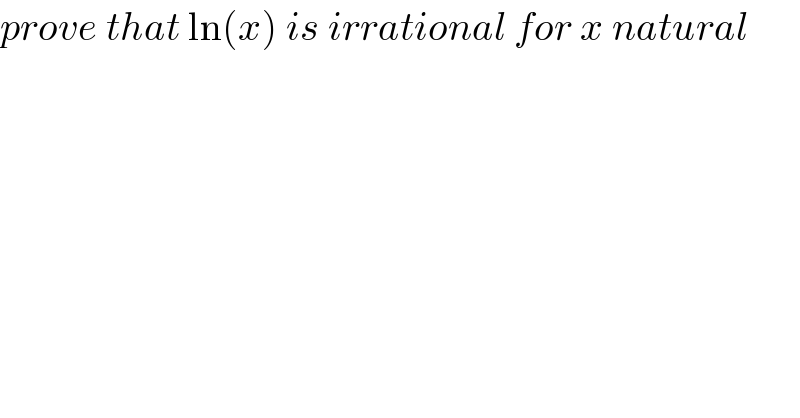
$${prove}\:{that}\:\mathrm{ln}\left({x}\right)\:{is}\:{irrational}\:{for}\:{x}\:{natural} \\ $$
Commented by math khazana by abdo last updated on 21/Jul/18
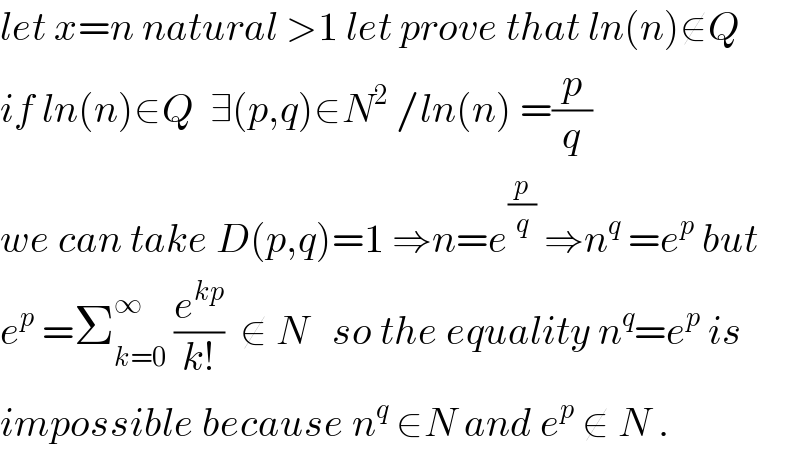
$${let}\:{x}={n}\:{natural}\:>\mathrm{1}\:{let}\:{prove}\:{that}\:{ln}\left({n}\right)\notin{Q} \\ $$$${if}\:{ln}\left({n}\right)\in{Q}\:\:\exists\left({p},{q}\right)\in{N}^{\mathrm{2}} \:/{ln}\left({n}\right)\:=\frac{{p}}{{q}} \\ $$$${we}\:{can}\:{take}\:{D}\left({p},{q}\right)=\mathrm{1}\:\Rightarrow{n}={e}^{\frac{{p}}{{q}}} \:\Rightarrow{n}^{{q}} \:={e}^{{p}} \:{but} \\ $$$${e}^{{p}} \:=\sum_{{k}=\mathrm{0}} ^{\infty} \:\frac{{e}^{{kp}} }{{k}!}\:\:\notin\:{N}\:\:\:{so}\:{the}\:{equality}\:{n}^{{q}} ={e}^{{p}} \:{is} \\ $$$${impossible}\:{because}\:{n}^{{q}} \:\in{N}\:{and}\:{e}^{{p}} \:\notin\:{N}\:. \\ $$
Commented by vitlu last updated on 21/Jul/18

$${thanks} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 21/Jul/18

$${you}\:{are}\:{wecome} \\ $$
