Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 195325 by mathlove last updated on 30/Jul/23

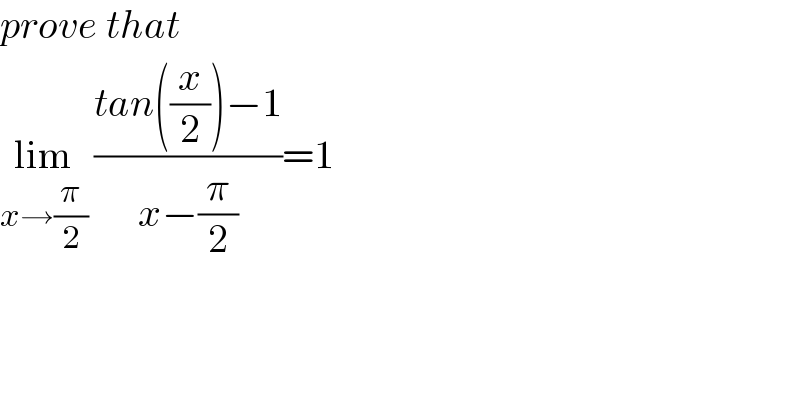
prove that lim_(x→(π/2)) ((tan((x/2))−1)/(x−(π/2)))=1

$${prove}\:{that} \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{{tan}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}}{{x}−\frac{\pi}{\mathrm{2}}}=\mathrm{1} \\ $$

Answered by BaliramKumar last updated on 30/Jul/23

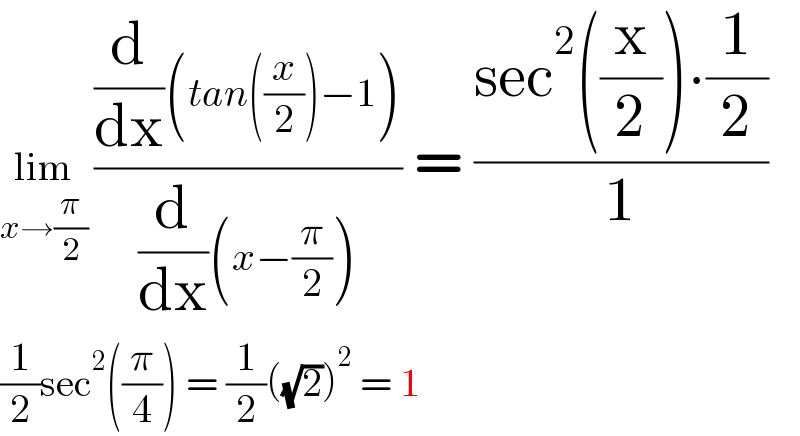
lim_(x→(π/2)) (((d/dx)(tan((x/2))−1))/((d/dx)(x−(π/2)))) = ((sec^2 ((x/2))∙(1/2))/1) (1/2)sec^2 ((π/4)) = (1/2)((√2))^2 = 1

$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\frac{\mathrm{d}}{\mathrm{dx}}\left({tan}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}\right)}{\frac{\mathrm{d}}{\mathrm{dx}}\left({x}−\frac{\pi}{\mathrm{2}}\right)}\:=\:\frac{\mathrm{sec}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\centerdot\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:=\:\mathrm{1} \\ $$

Answered by som(math1967) last updated on 30/Jul/23

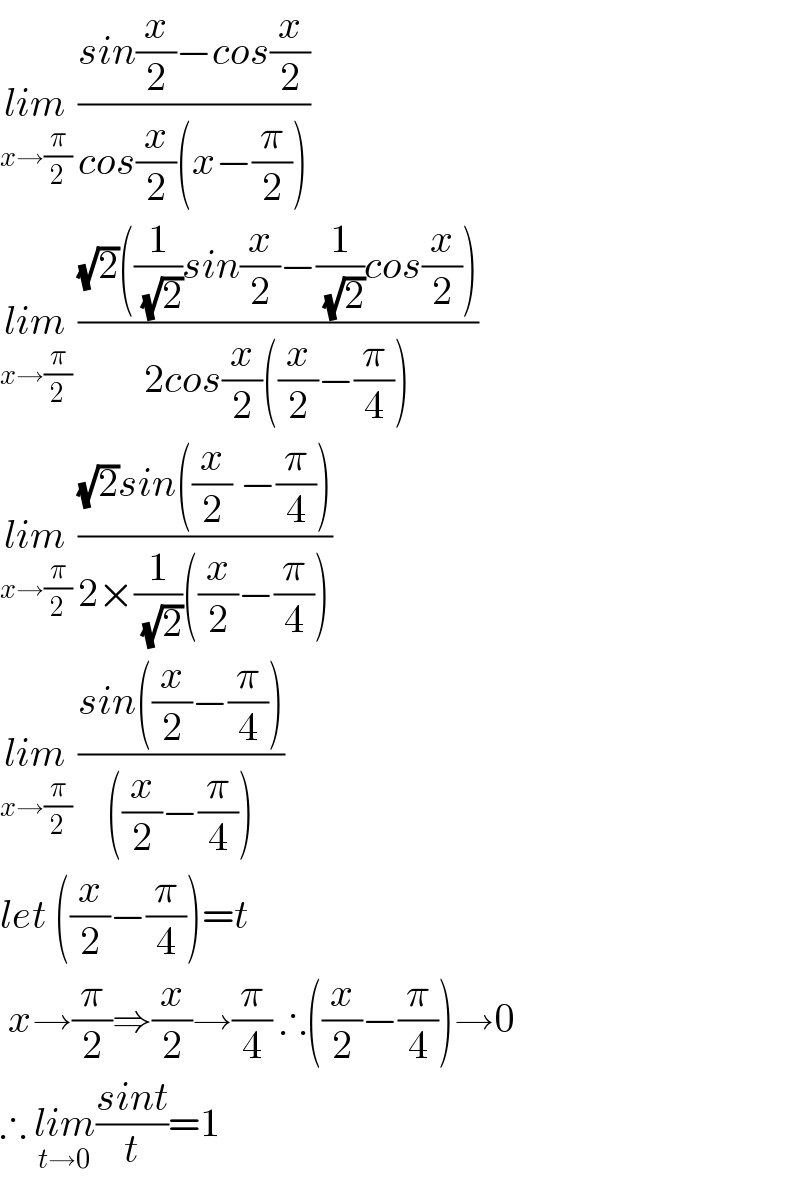
lim_(x→(π/2)) ((sin(x/2)−cos(x/2))/(cos(x/2)(x−(π/2)))) lim_(x→(π/2)) (((√2)((1/( (√2)))sin(x/2)−(1/( (√2)))cos(x/2)))/(2cos(x/2)((x/2)−(π/4)))) lim_(x→(π/2)) (((√2)sin((x/2) −(π/4)))/(2×(1/( (√2)))((x/2)−(π/4)))) lim_(x→(π/2)) ((sin((x/2)−(π/4)))/(((x/2)−(π/4)))) let ((x/2)−(π/4))=t x→(π/2)⇒(x/2)→(π/4) ∴((x/2)−(π/4))→0 ∴ lim_(t→0) ((sint)/t)=1

$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {{lim}}\:\frac{{sin}\frac{{x}}{\mathrm{2}}−{cos}\frac{{x}}{\mathrm{2}}}{{cos}\frac{{x}}{\mathrm{2}}\left({x}−\frac{\pi}{\mathrm{2}}\right)} \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {{lim}}\:\frac{\sqrt{\mathrm{2}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{sin}\frac{{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{cos}\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{cos}\frac{{x}}{\mathrm{2}}\left(\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right)} \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {{lim}}\:\frac{\sqrt{\mathrm{2}}{sin}\left(\frac{{x}}{\mathrm{2}}\:−\frac{\pi}{\mathrm{4}}\right)}{\mathrm{2}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right)} \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {{lim}}\:\frac{{sin}\left(\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right)}{\left(\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right)} \\ $$$${let}\:\left(\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right)={t} \\ $$$$\:{x}\rightarrow\frac{\pi}{\mathrm{2}}\Rightarrow\frac{{x}}{\mathrm{2}}\rightarrow\frac{\pi}{\mathrm{4}}\:\therefore\left(\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right)\rightarrow\mathrm{0} \\ $$$$\therefore\:\underset{{t}\rightarrow\mathrm{0}} {{lim}}\frac{{sint}}{{t}}=\mathrm{1} \\ $$

Commented by mathlove last updated on 30/Jul/23

tnks

$${tnks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com