
Question Number 78012 by malwaan last updated on 13/Jan/20
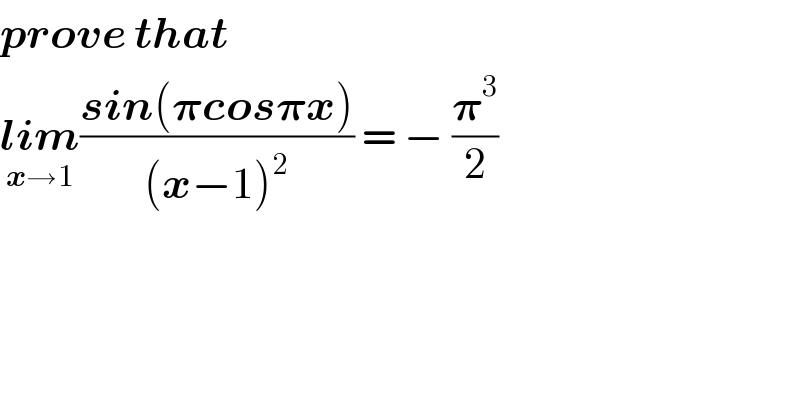
$$\boldsymbol{{prove}}\:\boldsymbol{{that}} \\ $$$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{1}} {\boldsymbol{{lim}}}\frac{\boldsymbol{{sin}}\left(\boldsymbol{\pi{cos}\pi{x}}\right)}{\left(\boldsymbol{{x}}−\mathrm{1}\right)^{\mathrm{2}} }\:=\:−\:\frac{\boldsymbol{\pi}^{\mathrm{3}} }{\mathrm{2}} \\ $$
Commented by msup trace by abdo last updated on 13/Jan/20
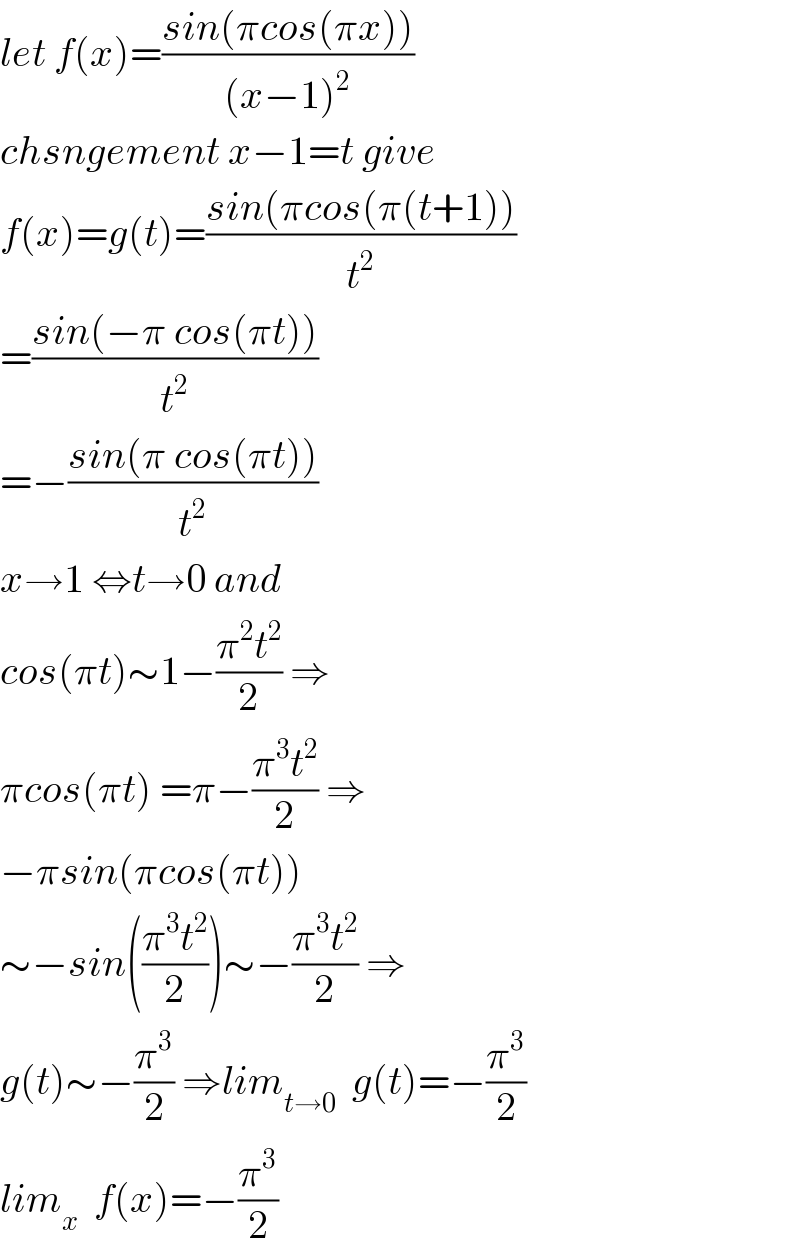
$${let}\:{f}\left({x}\right)=\frac{{sin}\left(\pi{cos}\left(\pi{x}\right)\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${chsngement}\:{x}−\mathrm{1}={t}\:{give} \\ $$$${f}\left({x}\right)={g}\left({t}\right)=\frac{{sin}\left(\pi{cos}\left(\pi\left({t}+\mathrm{1}\right)\right)\right.}{{t}^{\mathrm{2}} } \\ $$$$=\frac{{sin}\left(−\pi\:{cos}\left(\pi{t}\right)\right)}{{t}^{\mathrm{2}} } \\ $$$$=−\frac{{sin}\left(\pi\:{cos}\left(\pi{t}\right)\right)}{{t}^{\mathrm{2}} } \\ $$$${x}\rightarrow\mathrm{1}\:\Leftrightarrow{t}\rightarrow\mathrm{0}\:{and} \\ $$$${cos}\left(\pi{t}\right)\sim\mathrm{1}−\frac{\pi^{\mathrm{2}} {t}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\pi{cos}\left(\pi{t}\right)\:=\pi−\frac{\pi^{\mathrm{3}} {t}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$−\pi{sin}\left(\pi{cos}\left(\pi{t}\right)\right) \\ $$$$\sim−{sin}\left(\frac{\pi^{\mathrm{3}} {t}^{\mathrm{2}} }{\mathrm{2}}\right)\sim−\frac{\pi^{\mathrm{3}} {t}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$${g}\left({t}\right)\sim−\frac{\pi^{\mathrm{3}} }{\mathrm{2}}\:\Rightarrow{lim}_{{t}\rightarrow\mathrm{0}} \:\:{g}\left({t}\right)=−\frac{\pi^{\mathrm{3}} }{\mathrm{2}} \\ $$$${lim}_{{x}} \:\:{f}\left({x}\right)=−\frac{\pi^{\mathrm{3}} }{\mathrm{2}} \\ $$
Commented by john santu last updated on 13/Jan/20
![lim_(x→1) ((sin (π(−cos (π−πx)))/((x−1)^2 )) =lim_(y→0) ((sin (−πcos πy))/y^2 ) let −πcos πy = u ⇒cos πy=((−u)/π) πy=cos^(−1) (−(u/π)) ⇒y^2 =(1/π^2 )[cos^(−1) (((−u)/π))]^2 lim_(u→−π) ((π^2 sin (u))/([cos^(−1) (((−u)/π))]^2 )) =(π^2 /(−(2/π)))=−(π^3 /2)](Q78039.png)
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\pi\left(−\mathrm{cos}\:\left(\pi−\pi{x}\right)\right)\right.}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(−\pi\mathrm{cos}\:\pi{y}\right)}{{y}^{\mathrm{2}} } \\ $$$${let}\:−\pi\mathrm{cos}\:\pi{y}\:=\:{u}\:\Rightarrow\mathrm{cos}\:\pi{y}=\frac{−{u}}{\pi} \\ $$$$\pi{y}=\mathrm{cos}^{−\mathrm{1}} \left(−\frac{{u}}{\pi}\right)\:\Rightarrow{y}^{\mathrm{2}} =\frac{\mathrm{1}}{\pi^{\mathrm{2}} }\left[\mathrm{cos}^{−\mathrm{1}} \left(\frac{−{u}}{\pi}\right)\right]^{\mathrm{2}} \\ $$$$\underset{{u}\rightarrow−\pi} {\mathrm{lim}}\:\frac{\pi^{\mathrm{2}} \:\mathrm{sin}\:\left({u}\right)}{\left[\mathrm{cos}^{−\mathrm{1}} \left(\frac{−{u}}{\pi}\right)\right]^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{−\frac{\mathrm{2}}{\pi}}=−\frac{\pi^{\mathrm{3}} }{\mathrm{2}} \\ $$
Commented by malwaan last updated on 14/Jan/20

$$\boldsymbol{{thank}}\:\boldsymbol{{you}}\:\boldsymbol{{sir}} \\ $$
Answered by MJS last updated on 13/Jan/20
![...=lim_(x→1) (((d^2 /dx^2 )[sin (πcos (πx))])/((d^2 /dx^2 )[(x−1)^2 ]))= =lim_(x→1) ((−π^3 cos (πx) ×cos (πcos (πx)) −π^4 sin^2 (πx) ×sin (πcos (πx)))/2)= =−(π^3 /2)](Q78017.png)
$$...=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left[\mathrm{sin}\:\left(\pi\mathrm{cos}\:\left(\pi{x}\right)\right)\right]}{\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left[\left({x}−\mathrm{1}\right)^{\mathrm{2}} \right]}= \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{−\pi^{\mathrm{3}} \mathrm{cos}\:\left(\pi{x}\right)\:×\mathrm{cos}\:\left(\pi\mathrm{cos}\:\left(\pi{x}\right)\right)\:−\pi^{\mathrm{4}} \mathrm{sin}^{\mathrm{2}} \:\left(\pi{x}\right)\:×\mathrm{sin}\:\left(\pi\mathrm{cos}\:\left(\pi{x}\right)\right)}{\mathrm{2}}= \\ $$$$=−\frac{\pi^{\mathrm{3}} }{\mathrm{2}} \\ $$
Commented by malwaan last updated on 13/Jan/20
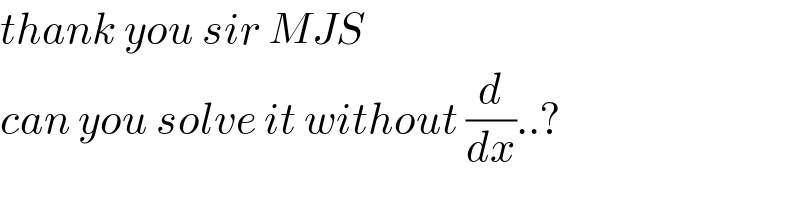
$${thank}\:{you}\:{sir}\:{MJS} \\ $$$${can}\:{you}\:{solve}\:{it}\:{without}\:\frac{{d}}{{dx}}..? \\ $$
