
Question Number 80000 by malwaan last updated on 30/Jan/20
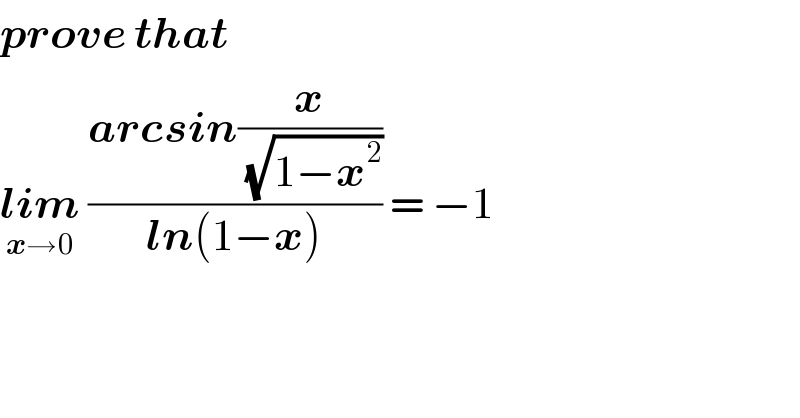
$$\boldsymbol{{prove}}\:\boldsymbol{{that}} \\ $$$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\:\frac{\boldsymbol{{arcsin}}\frac{\boldsymbol{{x}}}{\sqrt{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }}}{\boldsymbol{{ln}}\left(\mathrm{1}−\boldsymbol{{x}}\right)}\:=\:−\mathrm{1} \\ $$
Commented by jagoll last updated on 30/Jan/20
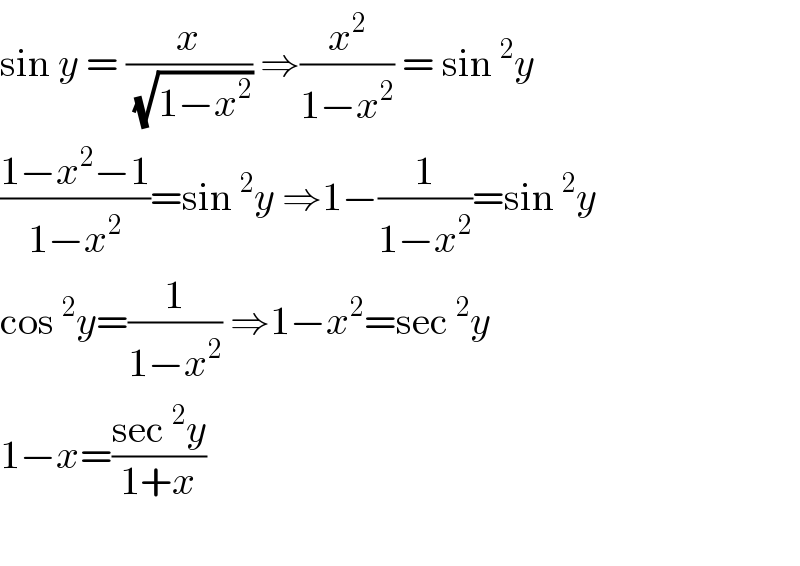
$$\mathrm{sin}\:{y}\:=\:\frac{{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\Rightarrow\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }\:=\:\mathrm{sin}\:^{\mathrm{2}} {y} \\ $$$$\frac{\mathrm{1}−{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }=\mathrm{sin}\:^{\mathrm{2}} {y}\:\Rightarrow\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }=\mathrm{sin}\:^{\mathrm{2}} {y} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} {y}=\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\:\Rightarrow\mathrm{1}−{x}^{\mathrm{2}} =\mathrm{sec}\:^{\mathrm{2}} {y} \\ $$$$\mathrm{1}−{x}=\frac{\mathrm{sec}\:^{\mathrm{2}} {y}}{\mathrm{1}+{x}} \\ $$$$ \\ $$
Commented by abdomathmax last updated on 30/Jan/20

$${let}\:{f}\left({x}\right)=\frac{{arcsin}\left(\frac{{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right)}{{ln}\left(\mathrm{1}−{x}\right)}\:\:{changement}\:{x}={sint}\: \\ $$$${give}\:{f}\left({x}\right)=\frac{{arcsin}\left({tant}\right)}{{ln}\left(\mathrm{1}−{sint}\right)}={g}\left({t}\right) \\ $$$${x}\rightarrow\mathrm{0}\:\Rightarrow{t}\rightarrow\mathrm{0}\:\:\:\Rightarrow\:{g}\left({t}\right)\sim\frac{{arcsint}}{−{t}}\:=−\frac{{arcsint}}{{t}} \\ $$$${and}\:{lim}_{{t}\rightarrow\mathrm{0}} \:\frac{{arsin}\left({t}\right)}{{t}}\:=\:{arcsin}^{'} \left(\mathrm{0}\right)\:\:{we}\:{have} \\ $$$${arcsin}^{'} \left({t}\right)\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:\Rightarrow{arcsin}^{'} \left(\mathrm{0}\right)\:=\mathrm{1}\:\Rightarrow \\ $$$${lim}_{{t}\rightarrow\mathrm{0}} \:{g}\left({t}\right)=−\mathrm{1}\:={lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right) \\ $$
Answered by Kamel Kamel last updated on 30/Jan/20
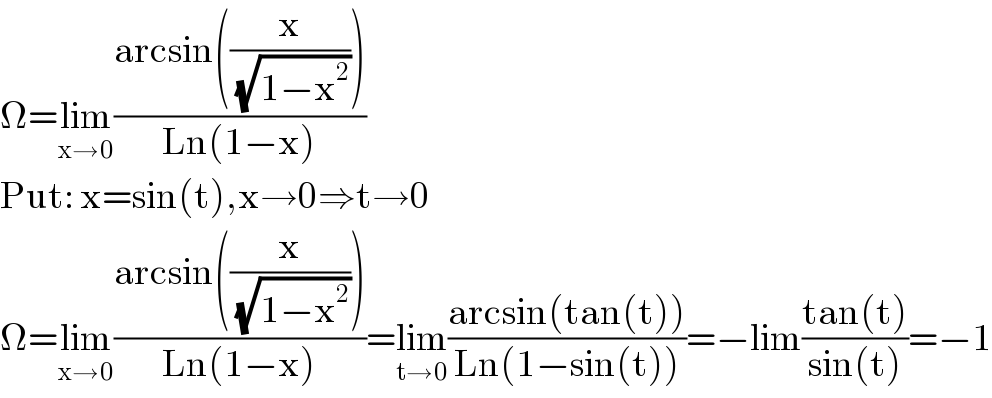
$$\Omega=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{arcsin}\left(\frac{\mathrm{x}}{\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\right)}{\mathrm{Ln}\left(\mathrm{1}−\mathrm{x}\right)} \\ $$$$\mathrm{Put}:\:\mathrm{x}=\mathrm{sin}\left(\mathrm{t}\right),\mathrm{x}\rightarrow\mathrm{0}\Rightarrow\mathrm{t}\rightarrow\mathrm{0} \\ $$$$\Omega=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{arcsin}\left(\frac{\mathrm{x}}{\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\right)}{\mathrm{Ln}\left(\mathrm{1}−\mathrm{x}\right)}=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{arcsin}\left(\mathrm{tan}\left(\mathrm{t}\right)\right)}{\mathrm{Ln}\left(\mathrm{1}−\mathrm{sin}\left(\mathrm{t}\right)\right)}=−\mathrm{lim}\frac{\mathrm{tan}\left(\mathrm{t}\right)}{\mathrm{sin}\left(\mathrm{t}\right)}=−\mathrm{1} \\ $$
Commented by malwaan last updated on 31/Jan/20
$${thank}\:{you}\:{so}\:{much} \\ $$
