
Question Number 192220 by gatocomcirrose last updated on 12/May/23

$$ \\ $$$$\mathrm{prove}\:\mathrm{that}\:\mathrm{if}\:\mathrm{n}\in\mathbb{N},\:\mathrm{n}>\mathrm{1}\:\mathrm{and}\:\mathrm{n}\:\mathrm{is}\:\mathrm{odd}\:\mathrm{then} \\ $$$$\:\mathrm{1}^{\mathrm{n}} +...+\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{n} \\ $$$$\left(\mathrm{dont}\:\mathrm{use}\:\equiv\left(\mathrm{modn}\right)\right) \\ $$
Commented by deleteduser1 last updated on 12/May/23
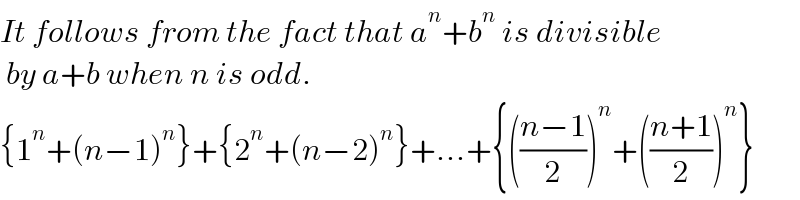
$${It}\:{follows}\:{from}\:{the}\:{fact}\:{that}\:{a}^{{n}} +{b}^{{n}} \:{is}\:{divisible} \\ $$$$\:{by}\:{a}+{b}\:{when}\:{n}\:{is}\:{odd}. \\ $$$$\left\{\mathrm{1}^{{n}} +\left({n}−\mathrm{1}\right)^{{n}} \right\}+\left\{\mathrm{2}^{{n}} +\left({n}−\mathrm{2}\right)^{{n}} \right\}+...+\left\{\left(\frac{{n}−\mathrm{1}}{\mathrm{2}}\right)^{{n}} +\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)^{{n}} \right\} \\ $$
Commented by gatocomcirrose last updated on 12/May/23
$$\mathrm{ohhhh}\:\mathrm{yeahh}\:\mathrm{thanks}\:\mathrm{bro} \\ $$
Answered by Frix last updated on 12/May/23
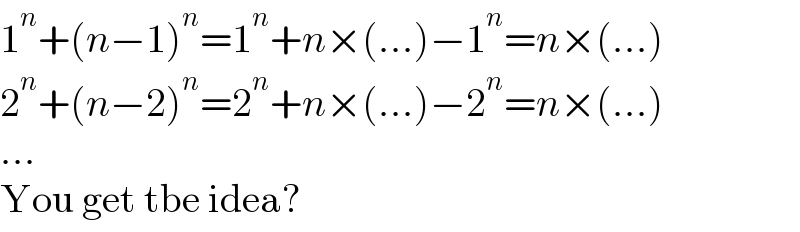
$$\mathrm{1}^{{n}} +\left({n}−\mathrm{1}\right)^{{n}} =\mathrm{1}^{{n}} +{n}×\left(...\right)−\mathrm{1}^{{n}} ={n}×\left(...\right) \\ $$$$\mathrm{2}^{{n}} +\left({n}−\mathrm{2}\right)^{{n}} =\mathrm{2}^{{n}} +{n}×\left(...\right)−\mathrm{2}^{{n}} ={n}×\left(...\right) \\ $$$$... \\ $$$$\mathrm{You}\:\mathrm{get}\:\mathrm{tbe}\:\mathrm{idea}? \\ $$
Commented by gatocomcirrose last updated on 12/May/23

$$\mathrm{yeah}\:\mathrm{thank}\:\mathrm{you}! \\ $$
