
Question Number 72344 by Rio Michael last updated on 27/Oct/19
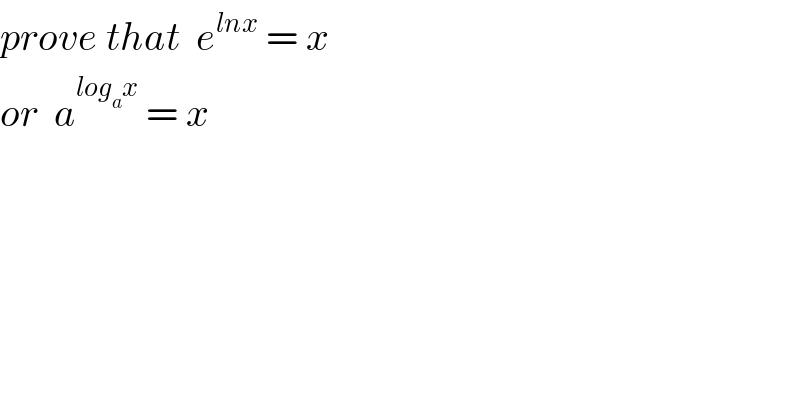
$${prove}\:{that}\:\:{e}^{{lnx}} \:=\:{x} \\ $$$${or}\:\:{a}^{{log}_{{a}} {x}} \:=\:{x} \\ $$
Commented by Prithwish sen last updated on 27/Oct/19

$$\boldsymbol{\mathrm{let}}\:\boldsymbol{\mathrm{lnx}}\:=\:\boldsymbol{\mathrm{M}} \\ $$$$\therefore\:\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{M}}} =\:\boldsymbol{\mathrm{x}} \\ $$$$\boldsymbol{\mathrm{putting}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{value}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{M}} \\ $$$$\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{lnx}}} \:=\:\boldsymbol{\mathrm{x}}\:\:\:\boldsymbol{\mathrm{proved}} \\ $$
Commented by Tony Lin last updated on 27/Oct/19

$${let}\:{log}_{{a}} {x}={y} \\ $$$${a}^{{y}} ={x} \\ $$$$\Rightarrow{log}_{{a}} {x}={y} \\ $$$$\Rightarrow{a}^{{log}_{{a}} {x}} ={x} \\ $$
Commented by Rio Michael last updated on 30/Oct/19

$${thank}\:{you}\:{sirs} \\ $$
