Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 86540 by jagoll last updated on 29/Mar/20

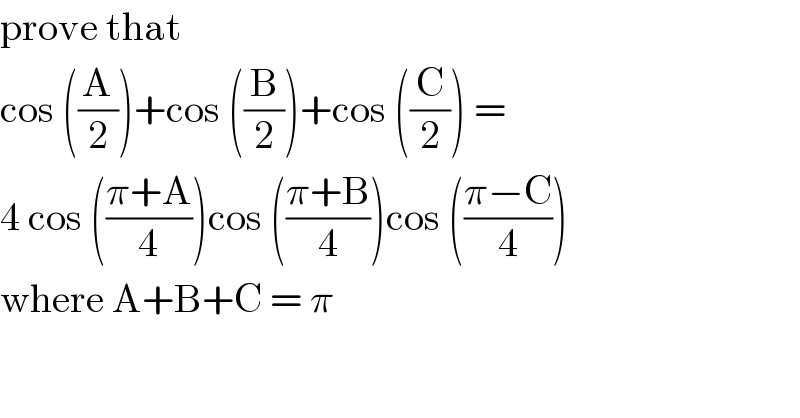
prove that cos ((A/2))+cos ((B/2))+cos ((C/2)) = 4 cos (((π+A)/4))cos (((π+B)/4))cos (((π−C)/4)) where A+B+C = π

$$\mathrm{prove}\:\mathrm{that} \\ $$$$\mathrm{cos}\:\left(\frac{\mathrm{A}}{\mathrm{2}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{B}}{\mathrm{2}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{C}}{\mathrm{2}}\right)\:=\: \\ $$$$\mathrm{4}\:\mathrm{cos}\:\left(\frac{\pi+\mathrm{A}}{\mathrm{4}}\right)\mathrm{cos}\:\left(\frac{\pi+\mathrm{B}}{\mathrm{4}}\right)\mathrm{cos}\:\left(\frac{\pi−\mathrm{C}}{\mathrm{4}}\right) \\ $$$$\mathrm{where}\:\mathrm{A}+\mathrm{B}+\mathrm{C}\:=\:\pi \\ $$

Commented by jagoll last updated on 29/Mar/20

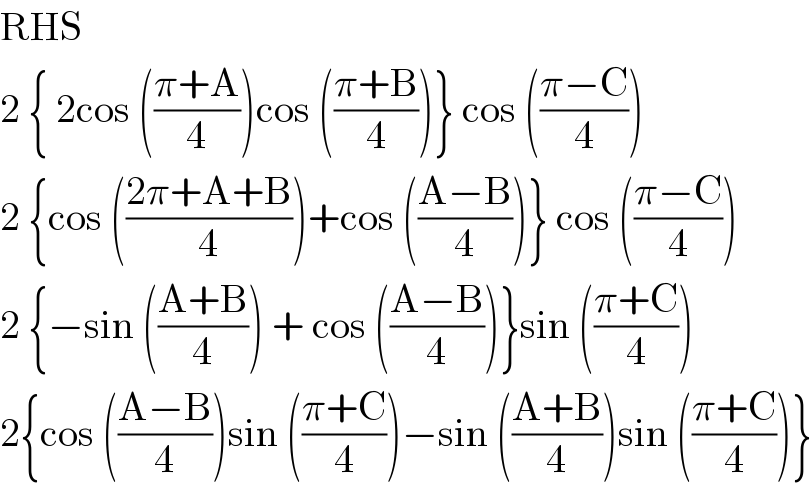
RHS 2 { 2cos (((π+A)/4))cos (((π+B)/4))} cos (((π−C)/4)) 2 {cos (((2π+A+B)/4))+cos (((A−B)/4))} cos (((π−C)/4)) 2 {−sin (((A+B)/4)) + cos (((A−B)/4))}sin (((π+C)/4)) 2{cos (((A−B)/4))sin (((π+C)/4))−sin (((A+B)/4))sin (((π+C)/4))}

$$\mathrm{RHS} \\ $$$$\mathrm{2}\:\left\{\:\mathrm{2cos}\:\left(\frac{\pi+\mathrm{A}}{\mathrm{4}}\right)\mathrm{cos}\:\left(\frac{\pi+\mathrm{B}}{\mathrm{4}}\right)\right\}\:\mathrm{cos}\:\left(\frac{\pi−\mathrm{C}}{\mathrm{4}}\right) \\ $$$$\mathrm{2}\:\left\{\mathrm{cos}\:\left(\frac{\mathrm{2}\pi+\mathrm{A}+\mathrm{B}}{\mathrm{4}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{A}−\mathrm{B}}{\mathrm{4}}\right)\right\}\:\mathrm{cos}\:\left(\frac{\pi−\mathrm{C}}{\mathrm{4}}\right) \\ $$$$\mathrm{2}\:\left\{−\mathrm{sin}\:\left(\frac{\mathrm{A}+\mathrm{B}}{\mathrm{4}}\right)\:+\:\mathrm{cos}\:\left(\frac{\mathrm{A}−\mathrm{B}}{\mathrm{4}}\right)\right\}\mathrm{sin}\:\left(\frac{\pi+\mathrm{C}}{\mathrm{4}}\right) \\ $$$$\mathrm{2}\left\{\mathrm{cos}\:\left(\frac{\mathrm{A}−\mathrm{B}}{\mathrm{4}}\right)\mathrm{sin}\:\left(\frac{\pi+\mathrm{C}}{\mathrm{4}}\right)−\mathrm{sin}\:\left(\frac{\mathrm{A}+\mathrm{B}}{\mathrm{4}}\right)\mathrm{sin}\:\left(\frac{\pi+\mathrm{C}}{\mathrm{4}}\right)\right\} \\ $$

Commented by john santu last updated on 29/Mar/20

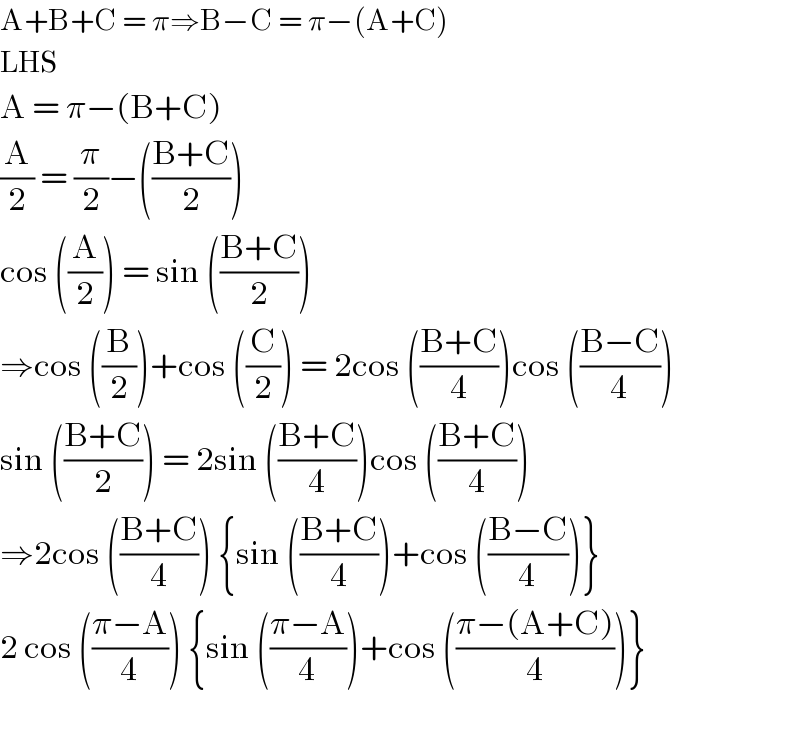
A+B+C = π⇒B−C = π−(A+C) LHS A = π−(B+C) (A/2) = (π/2)−(((B+C)/2)) cos ((A/2)) = sin (((B+C)/2)) ⇒cos ((B/2))+cos ((C/2)) = 2cos (((B+C)/4))cos (((B−C)/4)) sin (((B+C)/2)) = 2sin (((B+C)/4))cos (((B+C)/4)) ⇒2cos (((B+C)/4)) {sin (((B+C)/4))+cos (((B−C)/4))} 2 cos (((π−A)/4)) {sin (((π−A)/4))+cos (((π−(A+C))/4))}

$$\mathrm{A}+\mathrm{B}+\mathrm{C}\:=\:\pi\Rightarrow\mathrm{B}−\mathrm{C}\:=\:\pi−\left(\mathrm{A}+\mathrm{C}\right) \\ $$$$\mathrm{LHS} \\ $$$$\mathrm{A}\:=\:\pi−\left(\mathrm{B}+\mathrm{C}\right) \\ $$$$\frac{\mathrm{A}}{\mathrm{2}}\:=\:\frac{\pi}{\mathrm{2}}−\left(\frac{\mathrm{B}+\mathrm{C}}{\mathrm{2}}\right) \\ $$$$\mathrm{cos}\:\left(\frac{\mathrm{A}}{\mathrm{2}}\right)\:=\:\mathrm{sin}\:\left(\frac{\mathrm{B}+\mathrm{C}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mathrm{cos}\:\left(\frac{\mathrm{B}}{\mathrm{2}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{C}}{\mathrm{2}}\right)\:=\:\mathrm{2cos}\:\left(\frac{\mathrm{B}+\mathrm{C}}{\mathrm{4}}\right)\mathrm{cos}\:\left(\frac{\mathrm{B}−\mathrm{C}}{\mathrm{4}}\right) \\ $$$$\mathrm{sin}\:\left(\frac{\mathrm{B}+\mathrm{C}}{\mathrm{2}}\right)\:=\:\mathrm{2sin}\:\left(\frac{\mathrm{B}+\mathrm{C}}{\mathrm{4}}\right)\mathrm{cos}\:\left(\frac{\mathrm{B}+\mathrm{C}}{\mathrm{4}}\right) \\ $$$$\Rightarrow\mathrm{2cos}\:\left(\frac{\mathrm{B}+\mathrm{C}}{\mathrm{4}}\right)\:\left\{\mathrm{sin}\:\left(\frac{\mathrm{B}+\mathrm{C}}{\mathrm{4}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{B}−\mathrm{C}}{\mathrm{4}}\right)\right\} \\ $$$$\mathrm{2}\:\mathrm{cos}\:\left(\frac{\pi−\mathrm{A}}{\mathrm{4}}\right)\:\left\{\mathrm{sin}\:\left(\frac{\pi−\mathrm{A}}{\mathrm{4}}\right)+\mathrm{cos}\:\left(\frac{\pi−\left(\mathrm{A}+\mathrm{C}\right)}{\mathrm{4}}\right)\right\} \\ $$$$ \\ $$

Commented by jagoll last updated on 29/Mar/20

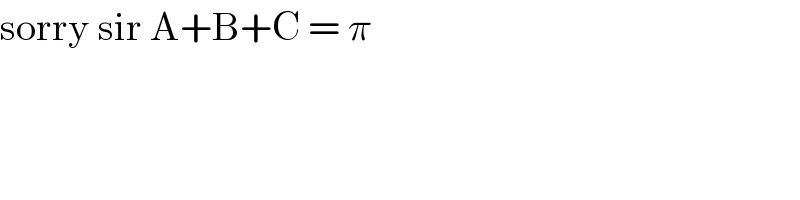
sorry sir A+B+C = π

$$\mathrm{sorry}\:\mathrm{sir}\:\mathrm{A}+\mathrm{B}+\mathrm{C}\:=\:\pi \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com