Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 204702 by mnjuly1970 last updated on 25/Feb/24

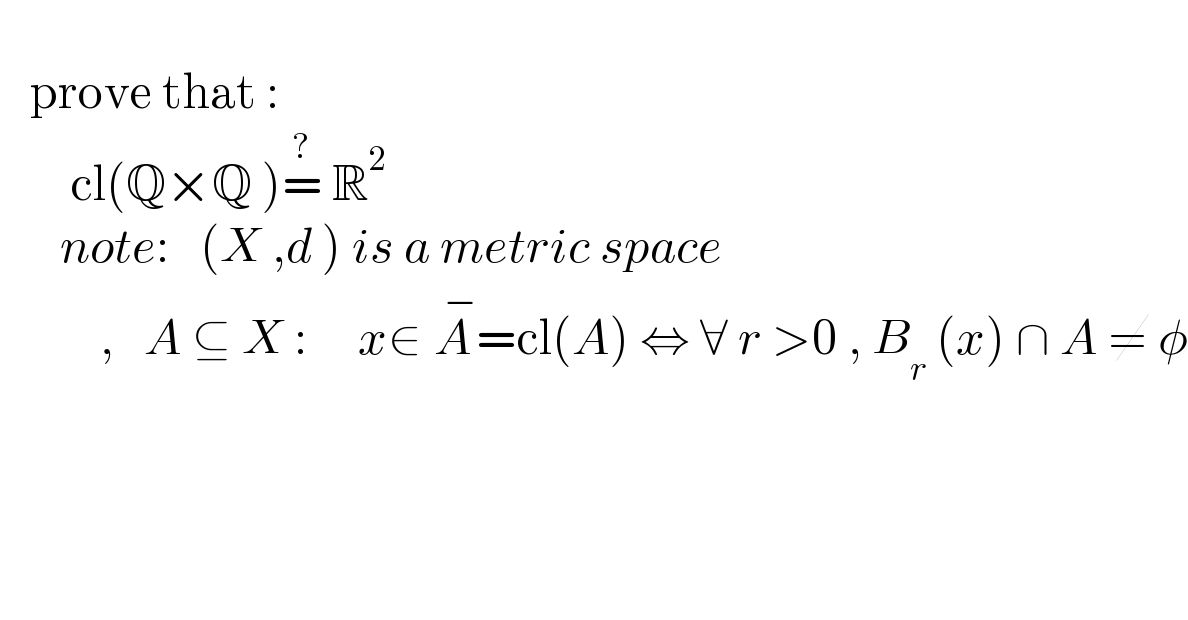
prove that : cl(Q×Q )=^? R^2 note: (X ,d ) is a metric space , A ⊆ X : x∈ A^( −) =cl(A) ⇔ ∀ r >0 , B_r (x) ∩ A ≠ φ

$$ \\ $$$$\:\:\:\mathrm{prove}\:\mathrm{that}\:: \\ $$$$\:\:\:\:\:\:\:\mathrm{cl}\left(\mathbb{Q}×\mathbb{Q}\:\right)\overset{?} {=}\:\mathbb{R}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:{note}:\:\:\:\left({X}\:,{d}\:\right)\:{is}\:{a}\:{metric}\:{space} \\ $$$$\:\:\:\:\:\:\:\:\:\:,\:\:\:{A}\:\subseteq\:{X}\::\:\:\:\:\:{x}\in\:\overset{\:\:−} {{A}}=\mathrm{cl}\left({A}\right)\:\Leftrightarrow\:\forall\:{r}\:>\mathrm{0}\:,\:{B}_{{r}} \:\left({x}\right)\:\cap\:{A}\:\neq\:\phi \\ $$

Answered by witcher3 last updated on 25/Feb/24

Q^− =R cl(Q∗Q)⊂Cl(Q^− ∗Q^− )=R^2 let x(a,b)∈R^2 =(x ⇒∃ U_n ,V_n ∈Q u_n →a;v_n →b ⇒∀ε>0 ∃N;∀n≥N ;∣U_n −a∣<ε;∀ε′>0 ∃N′∈N ;∀n≥N′∣V_n −b∣<0.....(1) since we are in finite dimensilm lets defind A metric?over R^2 d((x,y);(x′,y′))=max(∣x−x′∣;∣y−y′∣) let r>0 β_r (x) ∩Cl(Q^2 ) r>0 withe 1 ∃N_1 ,N_2 ∣u_n −a∣<r;∀n≥N_1 ∣u_n −b∣<r;∀n≥N_2 tack N=max(N_1 ,N_2 );∀n≥N d((u_n ,v_n );(a,b))=max(∣u_n −a∣;∣v_n −b∣)<r ⇒(a,b)∈cl(Q^2 ) ⇒IR^2 ⊂Cl(Q^2 )⇒equalitt

$$\overset{−} {\mathrm{Q}}=\mathbb{R} \\ $$$$\mathrm{cl}\left(\mathrm{Q}\ast\mathrm{Q}\right)\subset\mathrm{Cl}\left(\overset{−} {\mathrm{Q}}\ast\overset{−} {\mathrm{Q}}\right)=\mathbb{R}^{\mathrm{2}} \\ $$$$\mathrm{let}\:\mathrm{x}\left(\mathrm{a},\mathrm{b}\right)\in\mathbb{R}^{\mathrm{2}} =\left(\mathrm{x}\right. \\ $$$$\Rightarrow\exists\:\mathrm{U}_{\mathrm{n}} ,\mathrm{V}_{\mathrm{n}} \:\in\mathrm{Q} \\ $$$$\mathrm{u}_{\mathrm{n}} \rightarrow\mathrm{a};\mathrm{v}_{\mathrm{n}} \rightarrow\mathrm{b} \\ $$$$\Rightarrow\forall\epsilon>\mathrm{0}\:\exists\mathrm{N};\forall\mathrm{n}\geqslant\mathrm{N}\:;\mid\mathrm{U}_{\mathrm{n}} −\mathrm{a}\mid<\epsilon;\forall\epsilon'>\mathrm{0}\:\exists\mathrm{N}'\in\mathbb{N}\:;\forall\mathrm{n}\geqslant\mathrm{N}'\mid\mathrm{V}_{\mathrm{n}} −\mathrm{b}\mid<\mathrm{0}.....\left(\mathrm{1}\right) \\ $$$$\mathrm{since}\:\mathrm{we}\:\mathrm{are}\:\mathrm{in}\:\mathrm{finite}\:\mathrm{dimensilm} \\ $$$$\mathrm{lets}\:\mathrm{defind}\:\mathrm{A}\:\mathrm{metric}?\mathrm{over}\:\mathbb{R}^{\mathrm{2}} \\ $$$$\mathrm{d}\left(\left(\mathrm{x},\mathrm{y}\right);\left(\mathrm{x}',\mathrm{y}'\right)\right)=\mathrm{max}\left(\mid\mathrm{x}−\mathrm{x}'\mid;\mid\mathrm{y}−\mathrm{y}'\mid\right) \\ $$$$\mathrm{let}\:\mathrm{r}>\mathrm{0}\:\:\:\beta_{\mathrm{r}} \left(\mathrm{x}\right)\:\cap\mathrm{Cl}\left(\mathrm{Q}^{\mathrm{2}} \right) \\ $$$$\mathrm{r}>\mathrm{0}\:\mathrm{withe}\:\mathrm{1}\:\exists\mathrm{N}_{\mathrm{1}} ,\mathrm{N}_{\mathrm{2}} \\ $$$$\mid\mathrm{u}_{\mathrm{n}} −\mathrm{a}\mid<\mathrm{r};\forall\mathrm{n}\geqslant\mathrm{N}_{\mathrm{1}} \\ $$$$\mid\mathrm{u}_{\mathrm{n}} −\mathrm{b}\mid<\mathrm{r};\forall\mathrm{n}\geqslant\mathrm{N}_{\mathrm{2}} \\ $$$$\mathrm{tack}\:\mathrm{N}=\mathrm{max}\left(\mathrm{N}_{\mathrm{1}} ,\mathrm{N}_{\mathrm{2}} \right);\forall\mathrm{n}\geqslant\mathrm{N} \\ $$$$\mathrm{d}\left(\left(\mathrm{u}_{\mathrm{n}} ,\mathrm{v}_{\mathrm{n}} \right);\left(\mathrm{a},\mathrm{b}\right)\right)=\mathrm{max}\left(\mid\mathrm{u}_{\mathrm{n}} −\mathrm{a}\mid;\mid\mathrm{v}_{\mathrm{n}} −\mathrm{b}\mid\right)<\mathrm{r} \\ $$$$\Rightarrow\left(\mathrm{a},\mathrm{b}\right)\in\mathrm{cl}\left(\mathrm{Q}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{IR}^{\mathrm{2}} \subset\mathrm{Cl}\left(\mathrm{Q}^{\mathrm{2}} \right)\Rightarrow\mathrm{equalitt} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 25/Feb/24

thanks alot sir whicher

$${thanks}\:{alot}\:{sir}\:{whicher} \\ $$

Commented by witcher3 last updated on 25/Feb/24

withe pleasur barak alah Fikoum

$$\mathrm{withe}\:\mathrm{pleasur}\:\mathrm{barak}\:\mathrm{alah}\:\mathrm{Fikoum} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com