
Question Number 193767 by sciencestudentW last updated on 19/Jun/23
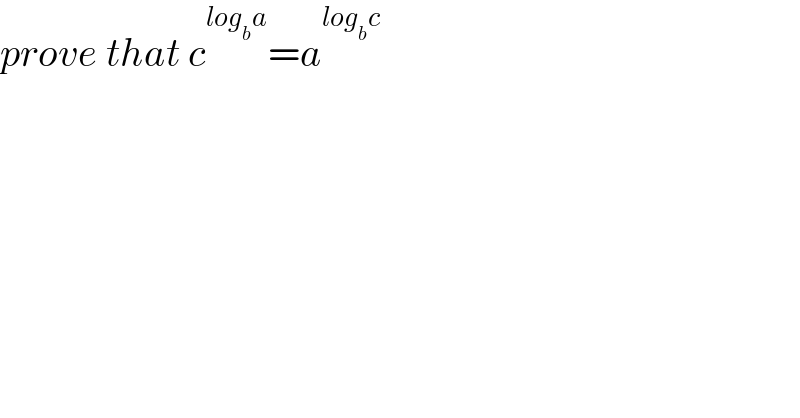
$${prove}\:{that}\:{c}^{{log}_{{b}} {a}} ={a}^{{log}_{{b}} {c}} \\ $$
Answered by deleteduser1 last updated on 19/Jun/23
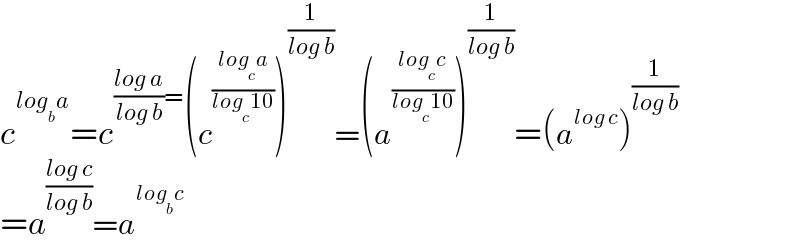
$${c}^{{log}_{{b}} {a}} ={c}^{\frac{{log}\:{a}}{{log}\:{b}}=} \left({c}^{\frac{{log}_{{c}} {a}}{{log}_{{c}} \mathrm{10}}} \right)^{\frac{\mathrm{1}}{{log}\:{b}}} =\left({a}^{\frac{{log}_{{c}} {c}}{{log}_{{c}} \mathrm{10}}} \right)^{\frac{\mathrm{1}}{{log}\:{b}}} =\left({a}^{{log}\:{c}} \right)^{\frac{\mathrm{1}}{{log}\:{b}}} \\ $$$$={a}^{\frac{{log}\:{c}}{{log}\:{b}}} ={a}^{{log}_{{b}} {c}} \\ $$
