
Question Number 190093 by mnjuly1970 last updated on 27/Mar/23
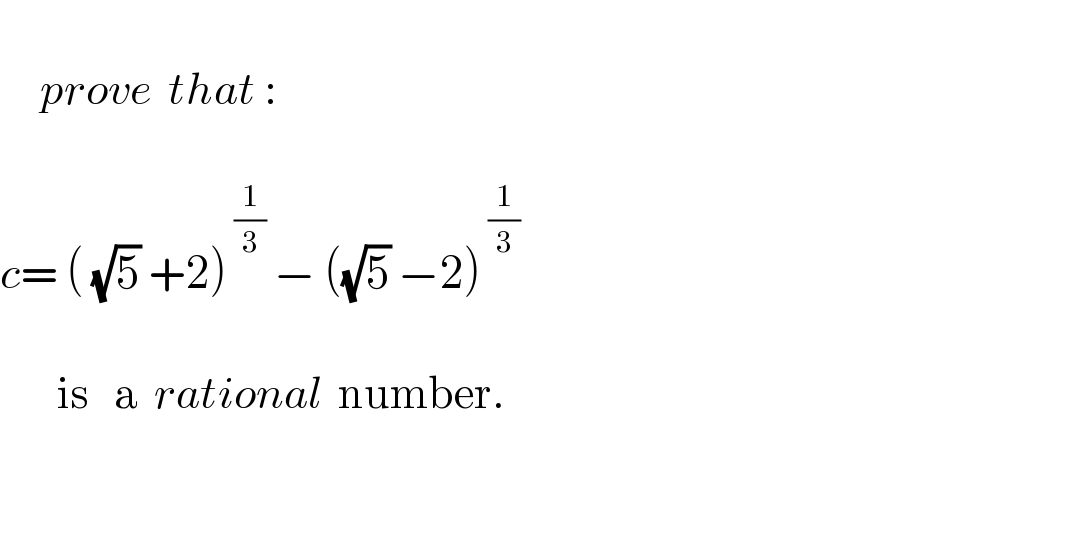
$$ \\ $$$$\:\:\:\:\:{prove}\:\:{that}\:: \\ $$$$ \\ $$$${c}=\:\left(\:\sqrt{\mathrm{5}}\:+\mathrm{2}\right)^{\:\frac{\mathrm{1}}{\mathrm{3}}} \:−\:\left(\sqrt{\mathrm{5}}\:−\mathrm{2}\right)^{\:\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\:\:\: \\ $$$$\:\:\:\:\:\:\:\mathrm{is}\:\:\:\mathrm{a}\:\:{rational}\:\:\mathrm{number}. \\ $$$$\:\:\:\:\: \\ $$$$\:\:\:\:\:\: \\ $$
Commented by MJS_new last updated on 27/Mar/23
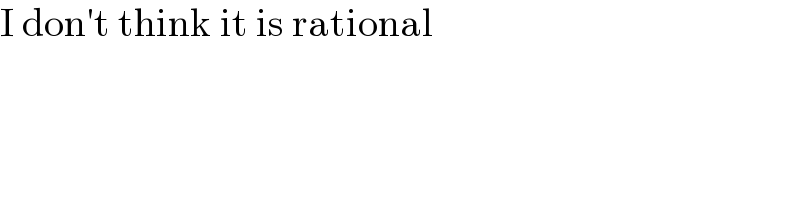
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{it}\:\mathrm{is}\:\mathrm{rational} \\ $$
Commented by som(math1967) last updated on 18/May/23
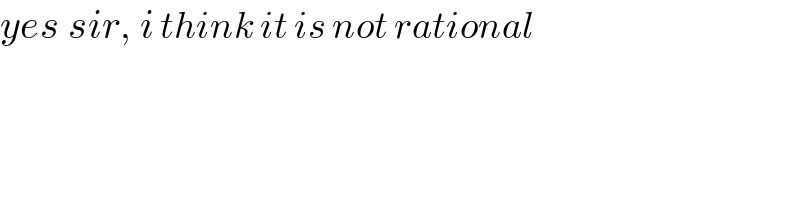
$${yes}\:{sir},\:{i}\:{think}\:{it}\:{is}\:{not}\:{rational} \\ $$
Commented by mnjuly1970 last updated on 27/Mar/23
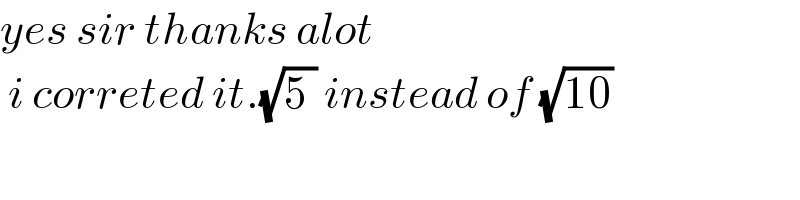
$${yes}\:{sir}\:{thanks}\:{alot} \\ $$$$\:{i}\:{correted}\:{it}.\sqrt{\mathrm{5}\:}\:{instead}\:{of}\:\sqrt{\mathrm{10}} \\ $$$$ \\ $$
Answered by MJS_new last updated on 27/Mar/23
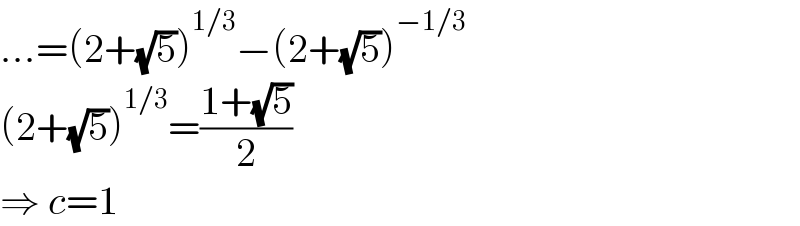
$$...=\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{1}/\mathrm{3}} −\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{−\mathrm{1}/\mathrm{3}} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{1}/\mathrm{3}} =\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow\:{c}=\mathrm{1} \\ $$
Answered by som(math1967) last updated on 27/Mar/23
![c^3 =((√5)+2)−((√5)−2)−3(5−4)^(1/3) .c [c=((√5)+2)^(1/3) −((√5)−2)^(1/3) ] c^3 =4−3c c^3 +3c−4=0 c^3 −1+3(c−1)=0 (c−1)(c^2 +c+1+3)=0 (c−1)(c^2 +c+4)=0 for real value of c (c^2 +c+4)≠0 c=1 ratinal number](Q190114.png)
$$\:{c}^{\mathrm{3}} =\left(\sqrt{\mathrm{5}}+\mathrm{2}\right)−\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)−\mathrm{3}\left(\mathrm{5}−\mathrm{4}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} .{c} \\ $$$$\left[{c}=\left(\sqrt{\mathrm{5}}+\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \right] \\ $$$${c}^{\mathrm{3}} =\mathrm{4}−\mathrm{3}{c} \\ $$$${c}^{\mathrm{3}} +\mathrm{3}{c}−\mathrm{4}=\mathrm{0} \\ $$$${c}^{\mathrm{3}} −\mathrm{1}+\mathrm{3}\left({c}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({c}−\mathrm{1}\right)\left({c}^{\mathrm{2}} +{c}+\mathrm{1}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\left({c}−\mathrm{1}\right)\left({c}^{\mathrm{2}} +{c}+\mathrm{4}\right)=\mathrm{0} \\ $$$${for}\:{real}\:{value}\:{of}\:{c}\:\:\left({c}^{\mathrm{2}} +{c}+\mathrm{4}\right)\neq\mathrm{0} \\ $$$${c}=\mathrm{1}\:{ratinal}\:{number} \\ $$
Commented by mehdee42 last updated on 27/Mar/23

$${that}\:{was}\:{perfect}. \\ $$
