
Question Number 75954 by mhmd last updated on 21/Dec/19
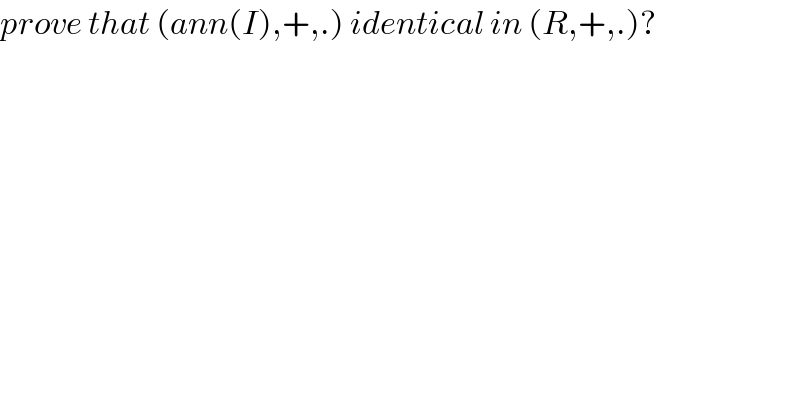
$${prove}\:{that}\:\left({ann}\left({I}\right),+,.\right)\:{identical}\:{in}\:\left({R},+,.\right)? \\ $$
Commented by kaivan.ahmadi last updated on 21/Dec/19

$${its}\:{a}\:{right}\:{ideal}\:{no}\:{identical} \\ $$
Commented by kaivan.ahmadi last updated on 21/Dec/19
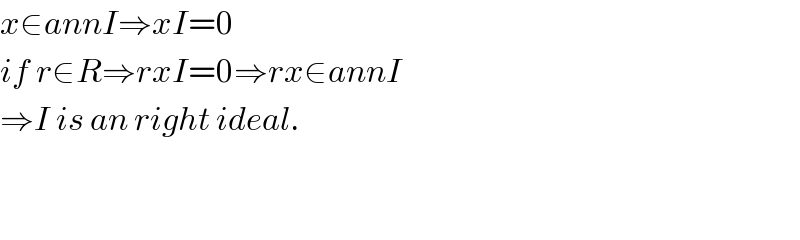
$${x}\in{annI}\Rightarrow{xI}=\mathrm{0} \\ $$$${if}\:{r}\in{R}\Rightarrow{rxI}=\mathrm{0}\Rightarrow{rx}\in{annI} \\ $$$$\Rightarrow{I}\:{is}\:{an}\:{right}\:{ideal}. \\ $$$$ \\ $$$$ \\ $$
