
Question Number 156761 by gsk2684 last updated on 15/Oct/21
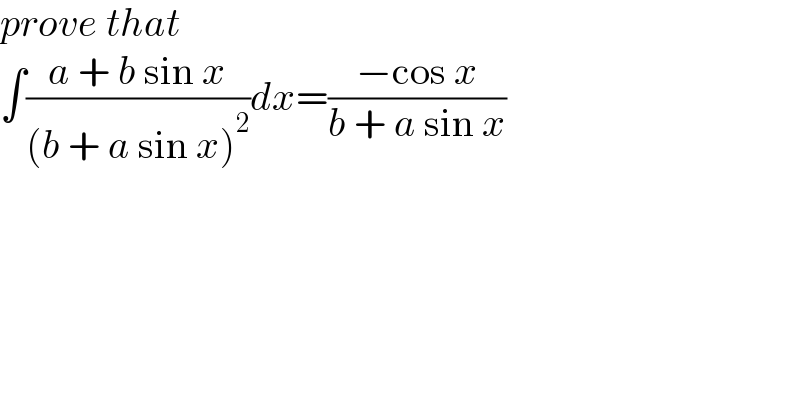
$${prove}\:{that} \\ $$$$\int\frac{{a}\:+\:{b}\:\mathrm{sin}\:{x}}{\left({b}\:+\:{a}\:\mathrm{sin}\:{x}\right)^{\mathrm{2}} }{dx}=\frac{−\mathrm{cos}\:{x}}{{b}\:+\:{a}\:\mathrm{sin}\:{x}} \\ $$
Answered by cortano last updated on 15/Oct/21
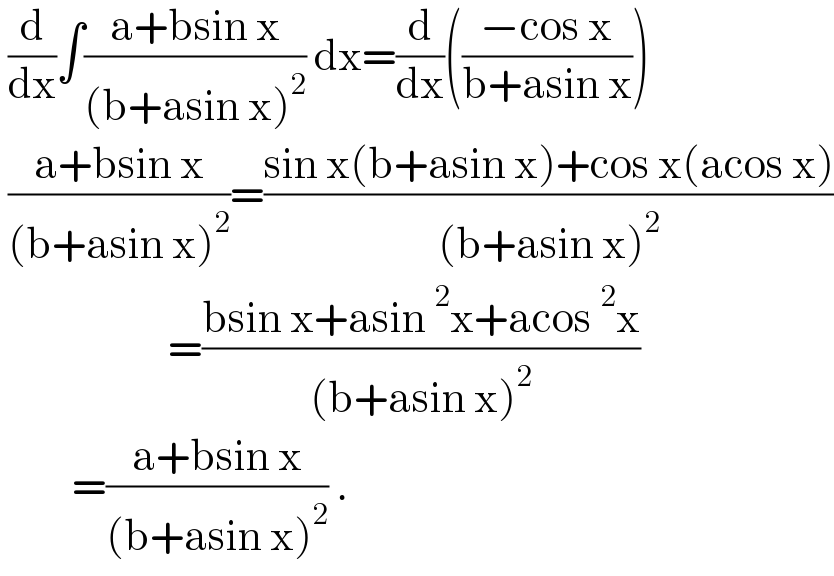
$$\:\frac{\mathrm{d}}{\mathrm{dx}}\int\frac{\mathrm{a}+\mathrm{bsin}\:\mathrm{x}}{\left(\mathrm{b}+\mathrm{asin}\:\mathrm{x}\right)^{\mathrm{2}} }\:\mathrm{dx}=\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{−\mathrm{cos}\:\mathrm{x}}{\mathrm{b}+\mathrm{asin}\:\mathrm{x}}\right) \\ $$$$\:\frac{\mathrm{a}+\mathrm{bsin}\:\mathrm{x}}{\left(\mathrm{b}+\mathrm{asin}\:\mathrm{x}\right)^{\mathrm{2}} }=\frac{\mathrm{sin}\:\mathrm{x}\left(\mathrm{b}+\mathrm{asin}\:\mathrm{x}\right)+\mathrm{cos}\:\mathrm{x}\left(\mathrm{acos}\:\mathrm{x}\right)}{\left(\mathrm{b}+\mathrm{asin}\:\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{bsin}\:\mathrm{x}+\mathrm{asin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{acos}\:^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{b}+\mathrm{asin}\:\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{a}+\mathrm{bsin}\:\mathrm{x}}{\left(\mathrm{b}+\mathrm{asin}\:\mathrm{x}\right)^{\mathrm{2}} }\:. \\ $$
Commented by gsk2684 last updated on 15/Oct/21
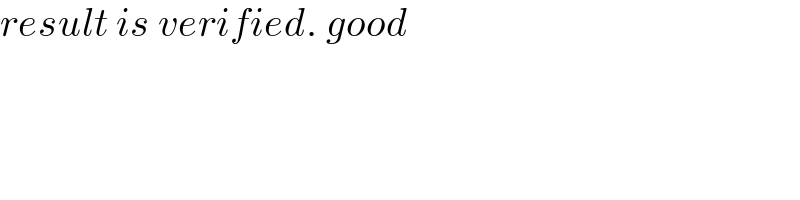
$${result}\:{is}\:{verified}.\:{good} \\ $$
Answered by puissant last updated on 15/Oct/21

$${D}\:=\:\int\frac{{a}+{bsinx}}{\left({b}+{asinx}\right)^{\mathrm{2}} }{dx}\:=\:\int\frac{\left({a}+{bsinx}\right)}{\left({b}+{asinx}\right)^{\mathrm{2}} }\bullet\frac{{sec}^{\mathrm{2}} {x}}{{sec}^{\mathrm{2}} {x}}{dx} \\ $$$$=\int\frac{{a}\:{sec}^{\mathrm{2}} {x}+{b}\:{tanx}\:{secx}}{\left({b}\:{secx}+{a}\:{tanx}\right)^{\mathrm{2}} }{dx} \\ $$$${u}={b}\:{secx}+{a}\:{tanx}\:\rightarrow\:{du}=\left({b}\:{secx}\:{tanx}+{a}\:{sec}^{\mathrm{2}} {x}\right){dx} \\ $$$$\Rightarrow\:{D}\:=\:\int\frac{{dt}}{{t}^{\mathrm{2}} }\:=\:\frac{−\mathrm{1}}{{t}}+{C}.. \\ $$$$\Rightarrow\:{D}\:=\:\frac{−\mathrm{1}}{{b}\:{secx}+{a}\:{tanx}}+{C} \\ $$$$\Rightarrow\:{D}\:=\:\frac{−\mathrm{1}}{\frac{{b}}{{cosx}}+\frac{{a}\:{sinx}}{{cosx}}}+{C}\:=\:\frac{−{cosx}}{{b}+{asinx}}\:+{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\therefore\because\:\:{D}\:=\:\frac{−{cosx}}{{b}+{a}\:{sinx}}+{C}.. \\ $$
Commented by gsk2684 last updated on 15/Oct/21

$${thank}\:{you} \\ $$
