
Question Number 44480 by peter frank last updated on 29/Sep/18
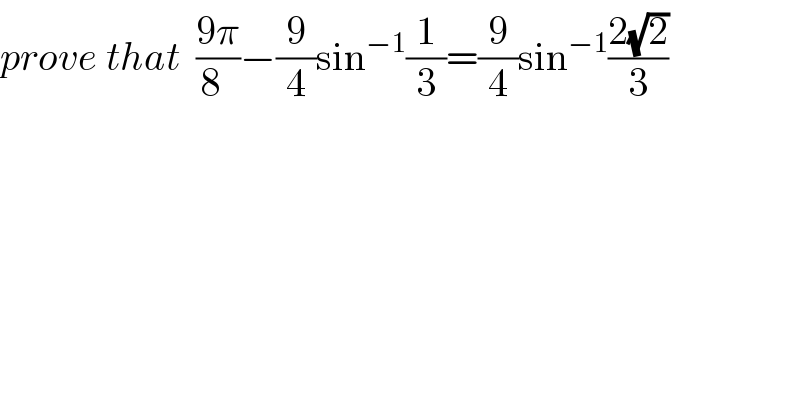
$${prove}\:{that}\:\:\frac{\mathrm{9}\pi}{\mathrm{8}\:\:}−\frac{\mathrm{9}}{\mathrm{4}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{9}}{\mathrm{4}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$
Answered by math1967 last updated on 30/Sep/18
![L.H.S=(9/4)((π/2)−sin^(−1) (1/3)) =(9/4)(cos^(−1) (1/3)) [∵sin^(−1) x+cos^(−1) x=(π/2)] =(9/4)sin^(−1) ((√(1−((1/3))^2 ))) =(9/4)sin^(−1) ((2(√2))/3)=R.H.S proved](Q44489.png)
$${L}.{H}.{S}=\frac{\mathrm{9}}{\mathrm{4}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{9}}{\mathrm{4}}\left(\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}\right)\:\:\:\:\:\:\:\left[\because\mathrm{sin}^{−\mathrm{1}} {x}+\mathrm{cos}^{−\mathrm{1}} {x}=\frac{\pi}{\mathrm{2}}\right] \\ $$$$=\frac{\mathrm{9}}{\mathrm{4}}\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{9}}{\mathrm{4}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}={R}.{H}.{S}\:{proved} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 29/Sep/18

$$\frac{\mathrm{9}}{\mathrm{4}}\left({sin}^{−\mathrm{1}} \frac{\mathrm{2}\sqrt{\mathrm{2}}\:}{\mathrm{3}}+{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\frac{\mathrm{9}}{\mathrm{4}}\left({tan}^{−\mathrm{1}} \frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{1}}+{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right) \\ $$$$\frac{\mathrm{9}}{\mathrm{4}}\left({tan}^{−\mathrm{1}} \frac{\mathrm{2}\sqrt{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}}{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}\:×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}}\right) \\ $$$$\frac{\mathrm{9}}{\mathrm{4}}{tan}^{−\mathrm{1}} \left(\infty\right) \\ $$$$\frac{\mathrm{9}}{\mathrm{4}}×\frac{\pi}{\mathrm{2}}=\frac{\mathrm{9}\pi}{\mathrm{8}} \\ $$$${so}\:\frac{\mathrm{9}\pi}{\mathrm{8}}−\frac{\mathrm{9}}{\mathrm{4}}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right)=\frac{\mathrm{9}}{\mathrm{4}}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:\:\:{proved} \\ $$
Commented by peter frank last updated on 29/Sep/18
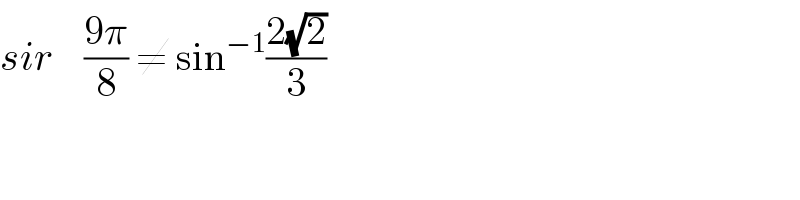
$${sir}\:\:\:\:\frac{\mathrm{9}\pi}{\mathrm{8}}\:\neq\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Sep/18
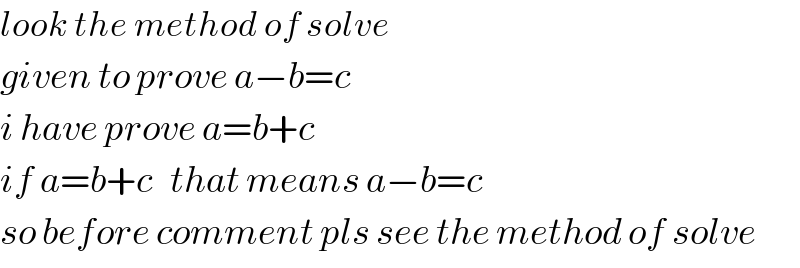
$${look}\:{the}\:{method}\:{of}\:{solve}\: \\ $$$${given}\:{to}\:{prove}\:{a}−{b}={c} \\ $$$${i}\:{have}\:{prove}\:{a}={b}+{c} \\ $$$${if}\:{a}={b}+{c}\:\:\:{that}\:{means}\:{a}−{b}={c} \\ $$$${so}\:{before}\:{comment}\:{pls}\:{see}\:{the}\:{method}\:{of}\:{solve} \\ $$
Commented by peter frank last updated on 29/Sep/18
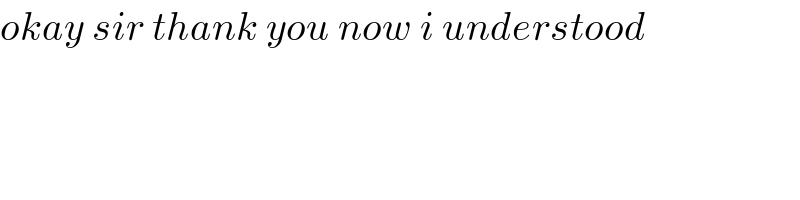
$${okay}\:{sir}\:{thank}\:{you}\:{now}\:{i}\:{understood} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Sep/18
![or method to prove ((9π)/8)−(9/4)sin^(−1) (((2(√2))/3))=(9/4)sin^(−1) ((1/3)) let k=(9/4)((π/2)−sin^(−1) (((2(√2))/3)) ((4k)/9)=(π/2)−sin^(−1) (((2(√2))/3)) sin(((4k)/9))=sin{(π/2)−sin^(−1) (((2(√2))/3))} sin(((4k)/9))=cos({sin^(−1) (((2(√2))/3))} sin(((4k)/9))=(1/3) [reason sinα=((2(√2))/3) so cosα=(1/3)] ((4k)/9)=sin^(−1) ((1/3)) k=(9/4)sin^(−1) ((1/3)) hence prlved...](Q44487.png)
$${or}\:{method} \\ $$$${to}\:{prove} \\ $$$$\frac{\mathrm{9}\pi}{\mathrm{8}}−\frac{\mathrm{9}}{\mathrm{4}}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right)=\frac{\mathrm{9}}{\mathrm{4}}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$${let}\:{k}=\frac{\mathrm{9}}{\mathrm{4}}\left(\frac{\pi}{\mathrm{2}}−{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right)\right. \\ $$$$\frac{\mathrm{4}{k}}{\mathrm{9}}=\frac{\pi}{\mathrm{2}}−{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right) \\ $$$${sin}\left(\frac{\mathrm{4}{k}}{\mathrm{9}}\right)={sin}\left\{\frac{\pi}{\mathrm{2}}−{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right)\right\} \\ $$$${sin}\left(\frac{\mathrm{4}{k}}{\mathrm{9}}\right)={cos}\left(\left\{{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right)\right\}\right. \\ $$$${sin}\left(\frac{\mathrm{4}{k}}{\mathrm{9}}\right)=\frac{\mathrm{1}}{\mathrm{3}}\:\:\left[{reason}\:\:{sin}\alpha=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\:\:\:{so}\:{cos}\alpha=\frac{\mathrm{1}}{\mathrm{3}}\right] \\ $$$$\frac{\mathrm{4}{k}}{\mathrm{9}}={sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$${k}=\frac{\mathrm{9}}{\mathrm{4}}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:\:\:{hence}\:{prlved}... \\ $$
Commented by peter frank last updated on 29/Sep/18

$${very}\:{nice}\:\: \\ $$
