
Question Number 130846 by Eric002 last updated on 29/Jan/21
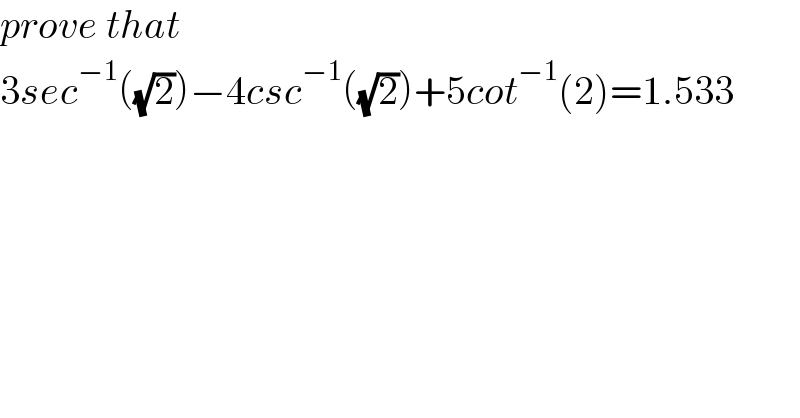
$${prove}\:{that} \\ $$$$\mathrm{3}{sec}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}\right)−\mathrm{4}{csc}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}\right)+\mathrm{5}{cot}^{−\mathrm{1}} \left(\mathrm{2}\right)=\mathrm{1}.\mathrm{533} \\ $$
Commented by MJS_new last updated on 30/Jan/21
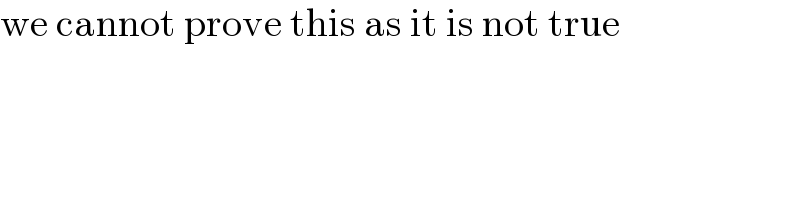
$$\mathrm{we}\:\mathrm{cannot}\:\mathrm{prove}\:\mathrm{this}\:\mathrm{as}\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{true} \\ $$
Answered by benjo_mathlover last updated on 30/Jan/21
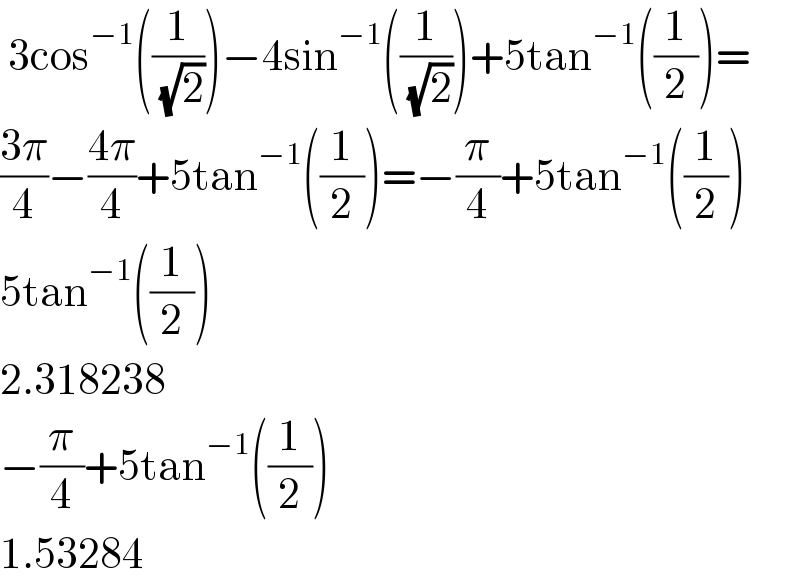
$$\:\mathrm{3cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)−\mathrm{4sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{5tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)= \\ $$$$\frac{\mathrm{3}\pi}{\mathrm{4}}−\frac{\mathrm{4}\pi}{\mathrm{4}}+\mathrm{5tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\frac{\pi}{\mathrm{4}}+\mathrm{5tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{5tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{2}.\mathrm{318238} \\ $$$$−\frac{\pi}{\mathrm{4}}+\mathrm{5tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{1}.\mathrm{53284} \\ $$
