Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 38557 by kunal1234523 last updated on 27/Jun/18

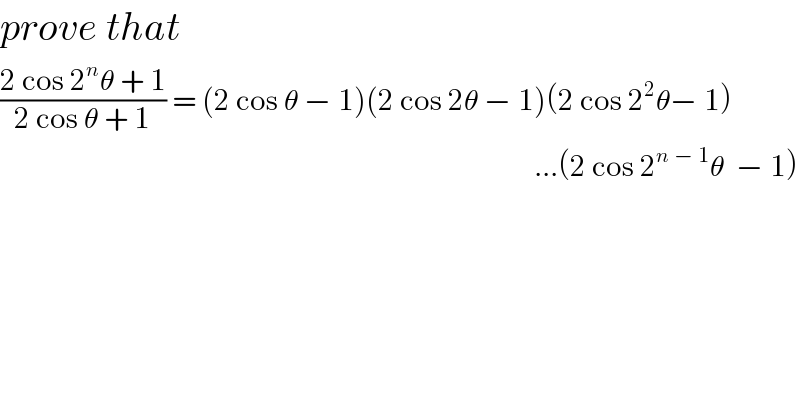
prove that ((2 cos 2^n θ + 1)/(2 cos θ + 1)) = (2 cos θ − 1)(2 cos 2θ − 1)(2 cos 2^2 θ− 1) ...(2 cos 2^(n − 1) θ − 1)

$${prove}\:{that} \\ $$$$\frac{\mathrm{2}\:\mathrm{cos}\:\mathrm{2}^{{n}} \theta\:+\:\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\theta\:+\:\mathrm{1}}\:=\:\left(\mathrm{2}\:\mathrm{cos}\:\theta\:−\:\mathrm{1}\right)\left(\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\theta\:−\:\mathrm{1}\right)\left(\mathrm{2}\:\mathrm{cos}\:\mathrm{2}^{\mathrm{2}} \theta−\:\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\left(\mathrm{2}\:\mathrm{cos}\:\mathrm{2}^{{n}\:−\:\mathrm{1}} \theta\:\:−\:\mathrm{1}\right) \\ $$

Answered by kunal1234523 last updated on 27/Jun/18

2 cos 2^x a + 1 =2 cos 2(2^(x−1) )a + 1 =2(2 cos^2 2^(x−1) a −1) + 1 =4 cos^2 2^(x−1) a −2 + 1 =(2 cos 2^(x−1) a)^2 − (1)^2 =(2 cos 2^(x−1) a + 1)(2 cos 2^(x−1) a −1) ........(1) L.H.S ((2 cos 2^n θ + 1)/(2 cos θ + 1)) from (1), taking x=n =(((2 cos 2^(n −1) a + 1)(2 cos 2^(n −1) a −1))/(2 cos a + 1)) now from (1), taking x=n−1 =(((2 cos 2^(n −2) a + 1)(2 cos 2^(n −2) a −1)(2 cos 2^(n −1) a −1))/(2 cos a + 1)) after some time =(((2 cos 2^(n −n) a + 1)(2 cos 2^(n −n) a −1)............(2 cos 2^(n −3) a −1)(2 cos 2^(n −2) a −1)(2 cos 2^(n −1) a −1))/(2 cos a + 1)) =(((2 cos a + 1)(2 cos a −1)(2 cos 2a −1)(2 cos 2^2 a −1)............(2 cos 2^(n −3) a −1)(2 cos 2^(n −2) a −1)(2 cos 2^(n −1) a −1))/((2 cos a + 1))) =(2 cos a −1)(2 cos 2a −1)(2 cos 2^2 a −1)............(2 cos 2^(n −3) a −1)(2 cos 2^(n −2) a −1)(2 cos 2^(n −1) a −1) proved

$$\mathrm{2}\:{cos}\:\mathrm{2}^{{x}} {a}\:+\:\mathrm{1} \\ $$$$=\mathrm{2}\:{cos}\:\mathrm{2}\left(\mathrm{2}^{{x}−\mathrm{1}} \right){a}\:+\:\mathrm{1} \\ $$$$=\mathrm{2}\left(\mathrm{2}\:{cos}^{\mathrm{2}} \:\mathrm{2}^{{x}−\mathrm{1}} {a}\:−\mathrm{1}\right)\:+\:\mathrm{1} \\ $$$$=\mathrm{4}\:{cos}^{\mathrm{2}} \:\mathrm{2}^{{x}−\mathrm{1}} {a}\:−\mathrm{2}\:+\:\mathrm{1} \\ $$$$=\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{x}−\mathrm{1}} {a}\right)^{\mathrm{2}} \:−\:\left(\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{x}−\mathrm{1}} {a}\:+\:\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{x}−\mathrm{1}} {a}\:−\mathrm{1}\right)\:........\left(\mathrm{1}\right) \\ $$$$\mathrm{L}.\mathrm{H}.\mathrm{S} \\ $$$$\frac{\mathrm{2}\:\mathrm{cos}\:\mathrm{2}^{{n}} \theta\:+\:\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\theta\:+\:\mathrm{1}} \\ $$$${from}\:\left(\mathrm{1}\right),\:{taking}\:{x}={n} \\ $$$$=\frac{\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−\mathrm{1}} {a}\:+\:\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−\mathrm{1}} {a}\:−\mathrm{1}\right)}{\mathrm{2}\:{cos}\:{a}\:+\:\mathrm{1}} \\ $$$${now}\:{from}\:\left(\mathrm{1}\right),\:{taking}\:{x}={n}−\mathrm{1} \\ $$$$=\frac{\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−\mathrm{2}} {a}\:+\:\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−\mathrm{2}} {a}\:−\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−\mathrm{1}} {a}\:−\mathrm{1}\right)}{\mathrm{2}\:{cos}\:{a}\:+\:\mathrm{1}} \\ $$$${after}\:{some}\:{time} \\ $$$$=\frac{\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−{n}} {a}\:+\:\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−{n}} {a}\:−\mathrm{1}\right)............\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−\mathrm{3}} {a}\:−\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−\mathrm{2}} {a}\:−\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−\mathrm{1}} {a}\:−\mathrm{1}\right)}{\mathrm{2}\:{cos}\:{a}\:+\:\mathrm{1}} \\ $$$$=\frac{\left(\mathrm{2}\:{cos}\:{a}\:+\:\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:{a}\:−\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}{a}\:−\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}^{\mathrm{2}} {a}\:−\mathrm{1}\right)............\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−\mathrm{3}} {a}\:−\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−\mathrm{2}} {a}\:−\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−\mathrm{1}} {a}\:−\mathrm{1}\right)}{\left(\mathrm{2}\:{cos}\:{a}\:+\:\mathrm{1}\right)} \\ $$$$=\left(\mathrm{2}\:{cos}\:{a}\:−\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}{a}\:−\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}^{\mathrm{2}} {a}\:−\mathrm{1}\right)............\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−\mathrm{3}} {a}\:−\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−\mathrm{2}} {a}\:−\mathrm{1}\right)\left(\mathrm{2}\:{cos}\:\mathrm{2}^{{n}\:−\mathrm{1}} {a}\:−\mathrm{1}\right) \\ $$$$\:{proved} \\ $$

Commented by kunal1234523 last updated on 05/Jul/18

is this right sir

$${is}\:{this}\:{right}\:{sir} \\ $$

Commented by math khazana by abdo last updated on 06/Jul/18

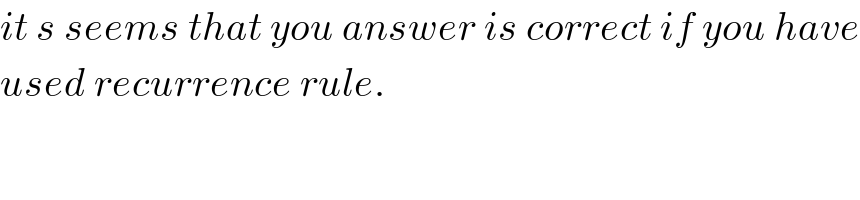
it s seems that you answer is correct if you have used recurrence rule.

$${it}\:{s}\:{seems}\:{that}\:{you}\:{answer}\:{is}\:{correct}\:{if}\:{you}\:{have} \\ $$$${used}\:{recurrence}\:{rule}. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com