
Question Number 193785 by aba last updated on 19/Jun/23
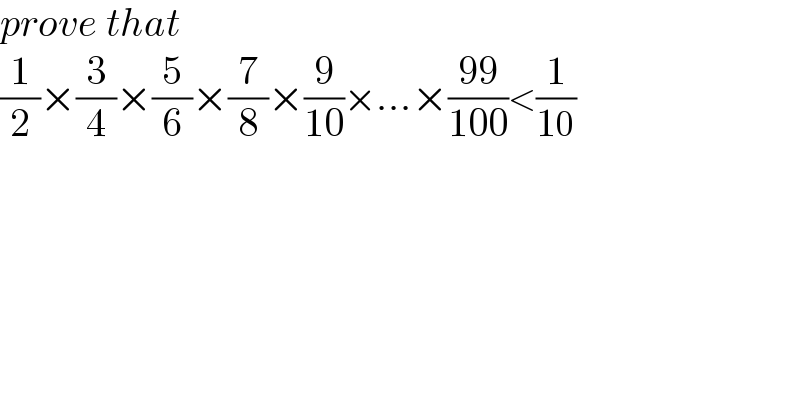
$${prove}\:{that} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{5}}{\mathrm{6}}×\frac{\mathrm{7}}{\mathrm{8}}×\frac{\mathrm{9}}{\mathrm{10}}×...×\frac{\mathrm{99}}{\mathrm{100}}<\frac{\mathrm{1}}{\mathrm{10}}\:\:\: \\ $$
Answered by MM42 last updated on 20/Jun/23
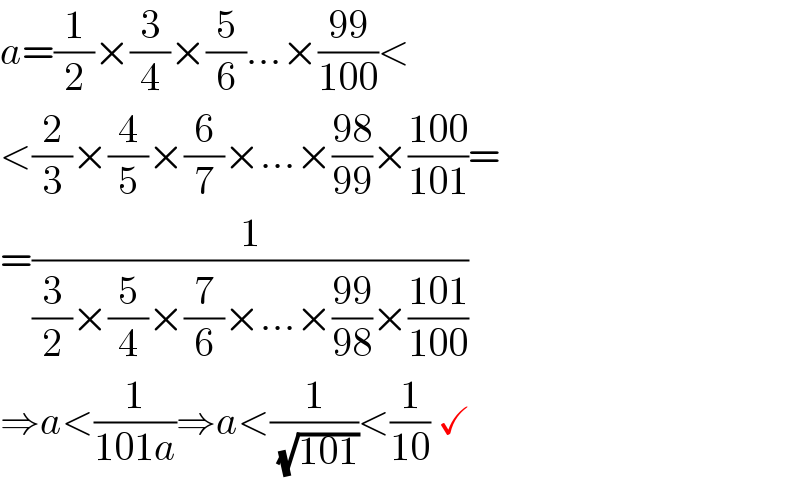
$${a}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{5}}{\mathrm{6}}...×\frac{\mathrm{99}}{\mathrm{100}}< \\ $$$$<\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{4}}{\mathrm{5}}×\frac{\mathrm{6}}{\mathrm{7}}×...×\frac{\mathrm{98}}{\mathrm{99}}×\frac{\mathrm{100}}{\mathrm{101}}= \\ $$$$=\frac{\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{5}}{\mathrm{4}}×\frac{\mathrm{7}}{\mathrm{6}}×...×\frac{\mathrm{99}}{\mathrm{98}}×\frac{\mathrm{101}}{\mathrm{100}}} \\ $$$$\Rightarrow{a}<\frac{\mathrm{1}}{\mathrm{101}{a}}\Rightarrow{a}<\frac{\mathrm{1}}{\:\sqrt{\mathrm{101}}}<\frac{\mathrm{1}}{\mathrm{10}}\:\checkmark \\ $$
Commented by aba last updated on 20/Jun/23

$$\mathrm{perfect} \\ $$
