Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 147071 by alcohol last updated on 17/Jul/21

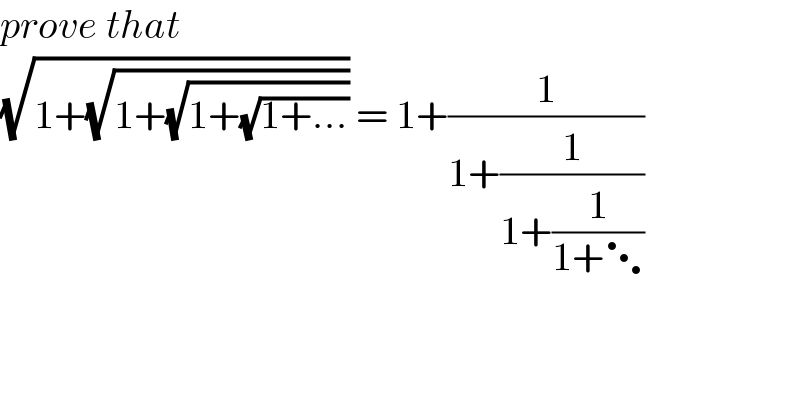
prove that (√(1+(√(1+(√(1+(√(1+...)))))))) = 1+(1/(1+(1/(1+(1/(1+⋱))))))

$${prove}\:{that} \\ $$$$\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+...}}}}\:=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\ddots}}} \\ $$

Answered by Olaf_Thorendsen last updated on 17/Jul/21

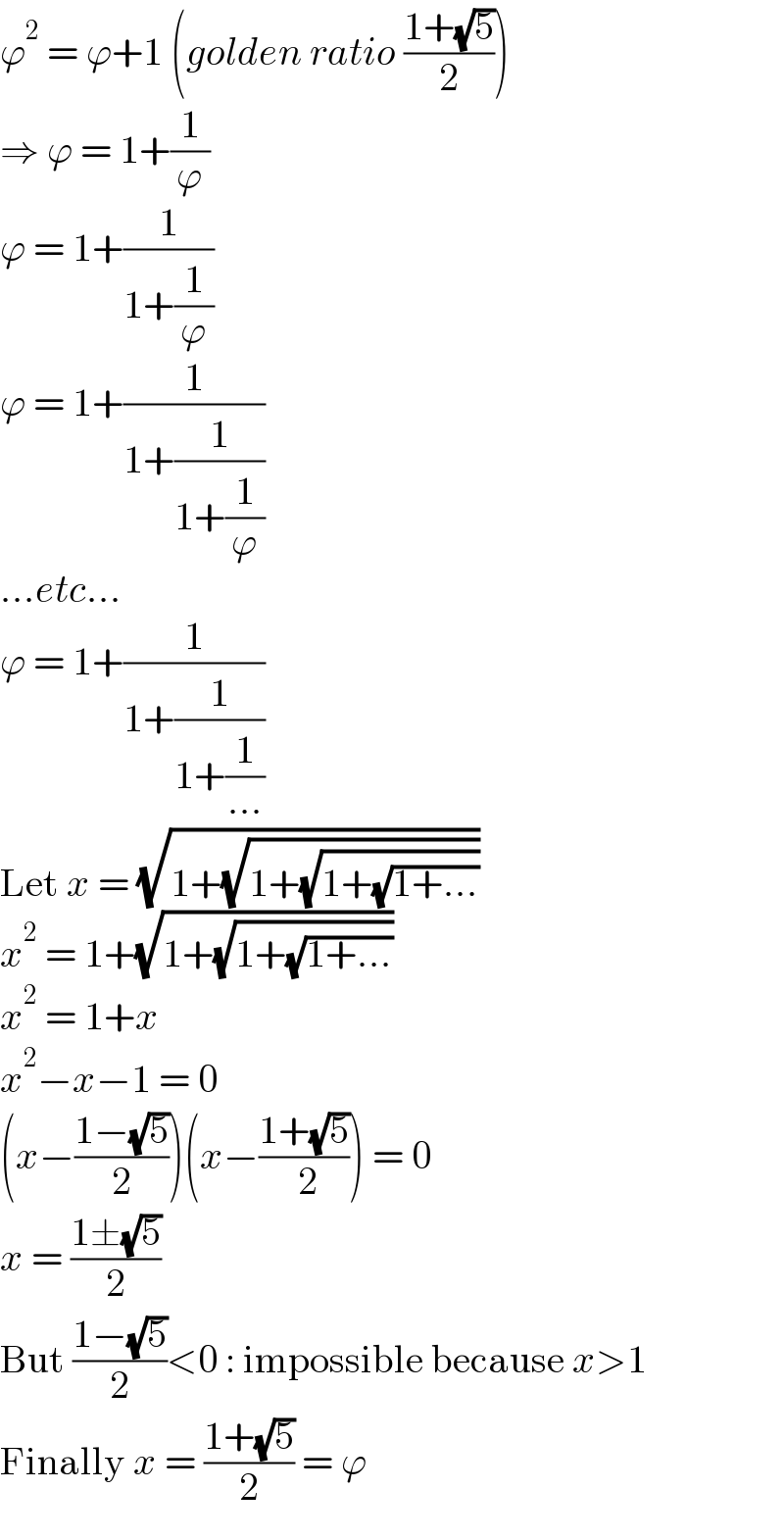
ϕ^2 = ϕ+1 (golden ratio ((1+(√5))/2)) ⇒ ϕ = 1+(1/ϕ) ϕ = 1+(1/(1+(1/ϕ))) ϕ = 1+(1/(1+(1/(1+(1/ϕ))))) ...etc... ϕ = 1+(1/(1+(1/(1+(1/(...)))))) Let x = (√(1+(√(1+(√(1+(√(1+...)))))))) x^2 = 1+(√(1+(√(1+(√(1+...)))))) x^2 = 1+x x^2 −x−1 = 0 (x−((1−(√5))/2))(x−((1+(√5))/( 2))) = 0 x = ((1±(√5))/2) But ((1−(√5))/2)<0 : impossible because x>1 Finally x = ((1+(√5))/2) = ϕ

$$\varphi^{\mathrm{2}} \:=\:\varphi+\mathrm{1}\:\left({golden}\:{ratio}\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\varphi\:=\:\mathrm{1}+\frac{\mathrm{1}}{\varphi} \\ $$$$\varphi\:=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\varphi}} \\ $$$$\varphi\:=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\varphi}}} \\ $$$$...{etc}... \\ $$$$\varphi\:=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{...}}} \\ $$$$\mathrm{Let}\:{x}\:=\:\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+...}}}} \\ $$$${x}^{\mathrm{2}} \:=\:\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+...}}} \\ $$$${x}^{\mathrm{2}} \:=\:\mathrm{1}+{x} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\left({x}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\left({x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\:\mathrm{2}}\right)\:=\:\mathrm{0} \\ $$$${x}\:=\:\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{But}\:\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}<\mathrm{0}\::\:\mathrm{impossible}\:\mathrm{because}\:{x}>\mathrm{1} \\ $$$$\mathrm{Finally}\:{x}\:=\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:=\:\varphi \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com