
Question Number 166113 by mathls last updated on 13/Feb/22

$${prove}\:{that}\:\mathrm{1}!=\mathrm{1} \\ $$
Commented by mathls last updated on 13/Feb/22

$$? \\ $$
Commented by MJS_new last updated on 14/Feb/22
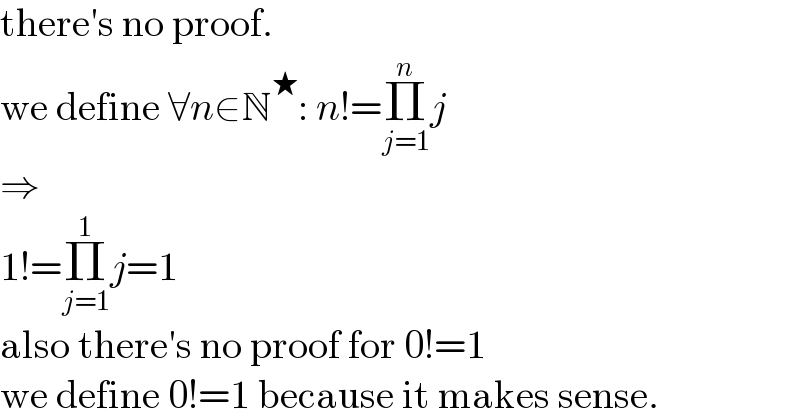
$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{proof}. \\ $$$$\mathrm{we}\:\mathrm{define}\:\forall{n}\in\mathbb{N}^{\bigstar} :\:{n}!=\underset{{j}=\mathrm{1}} {\overset{{n}} {\prod}}{j} \\ $$$$\Rightarrow \\ $$$$\mathrm{1}!=\underset{{j}=\mathrm{1}} {\overset{\mathrm{1}} {\prod}}{j}=\mathrm{1} \\ $$$$\mathrm{also}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{proof}\:\mathrm{for}\:\mathrm{0}!=\mathrm{1} \\ $$$$\mathrm{we}\:\mathrm{define}\:\mathrm{0}!=\mathrm{1}\:\mathrm{because}\:\mathrm{it}\:\mathrm{makes}\:\mathrm{sense}. \\ $$
Answered by alephzero last updated on 14/Feb/22

$${n}!\:=\:{n}\:\centerdot\:\left({n}−\mathrm{1}\right)! \\ $$$$\mathrm{Let}\:{n}\:=\:\mathrm{2} \\ $$$$\Rightarrow\:\mathrm{2}!\:=\:\mathrm{2}\:\centerdot\:\mathrm{1}! \\ $$$$\Rightarrow\:\mathrm{2}\:=\:\mathrm{2}\:\centerdot\:\mathrm{1}! \\ $$$$\Rightarrow\:\mathrm{1}!\:=\:\mathrm{1} \\ $$
Answered by Mathspace last updated on 14/Feb/22
![1!=Γ(2)=∫_0 ^∞ t^(2−1) e^(−t) dt =∫_0 ^∞ t e^(−t) dt=[−te^(−t) ]_0 ^∞ +∫_0 ^∞ e^(−t) dt =[−e^(−t) ]_0 ^∞ =1 0!=Γ(1)=∫_0 ^∞ t^(1−1) e^(−t) dt =∫_0 ^∞ e^(−t) dt=[−e^(−t) ]_0 ^∞ =1](Q166154.png)
$$\mathrm{1}!=\Gamma\left(\mathrm{2}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{2}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:{t}\:{e}^{−{t}} {dt}=\left[−{te}^{−{t}} \right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} {dt} \\ $$$$=\left[−{e}^{−{t}} \right]_{\mathrm{0}} ^{\infty} =\mathrm{1} \\ $$$$\mathrm{0}!=\Gamma\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{1}−\mathrm{1}} \:{e}^{−{t}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {dt}=\left[−{e}^{−{t}} \right]_{\mathrm{0}} ^{\infty} =\mathrm{1} \\ $$
