Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 140310 by liberty last updated on 06/May/21

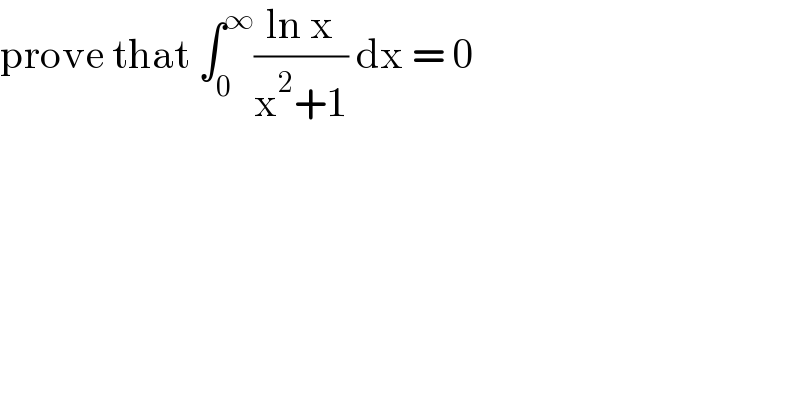
prove that ∫_0 ^∞ ((ln x)/(x^2 +1)) dx = 0

$$\mathrm{prove}\:\mathrm{that}\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{dx}\:=\:\mathrm{0} \\ $$

Answered by qaz last updated on 06/May/21

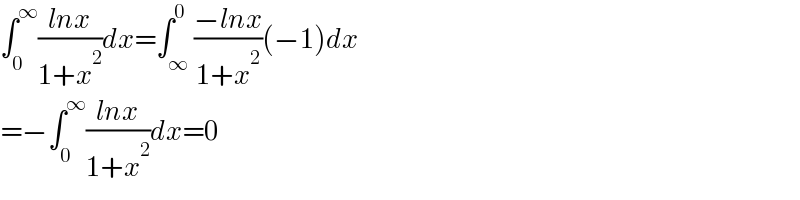
∫_0 ^∞ ((lnx)/(1+x^2 ))dx=∫_∞ ^0 ((−lnx)/(1+x^2 ))(−1)dx =−∫_0 ^∞ ((lnx)/(1+x^2 ))dx=0

$$\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\int_{\infty} ^{\mathrm{0}} \frac{−{lnx}}{\mathrm{1}+{x}^{\mathrm{2}} }\left(−\mathrm{1}\right){dx} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\mathrm{0} \\ $$

Commented by TheSupreme last updated on 06/May/21

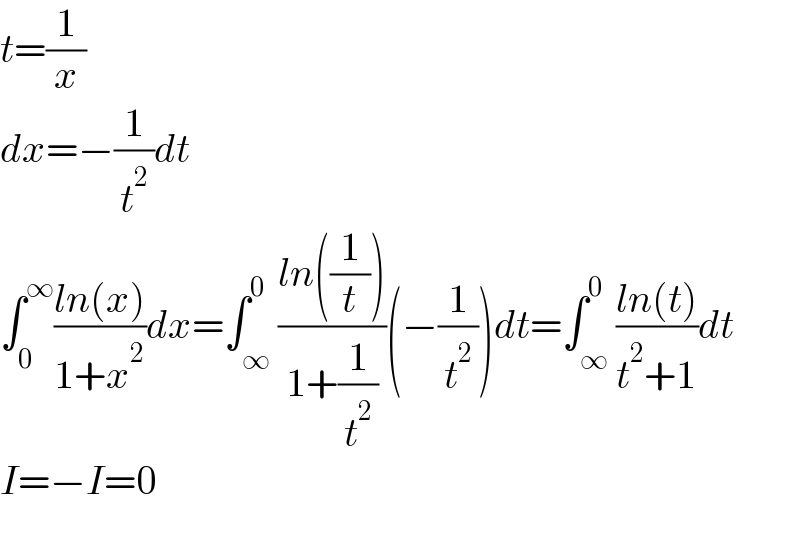
t=(1/x) dx=−(1/t^2 )dt ∫_0 ^∞ ((ln(x))/(1+x^2 ))dx=∫_∞ ^0 ((ln((1/t)))/(1+(1/t^2 )))(−(1/t^2 ))dt=∫_∞ ^0 ((ln(t))/(t^2 +1))dt I=−I=0

$${t}=\frac{\mathrm{1}}{{x}} \\ $$$${dx}=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\int_{\infty} ^{\mathrm{0}} \frac{{ln}\left(\frac{\mathrm{1}}{{t}}\right)}{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}\left(−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right){dt}=\int_{\infty} ^{\mathrm{0}} \frac{{ln}\left({t}\right)}{{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$${I}=−{I}=\mathrm{0} \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 06/May/21

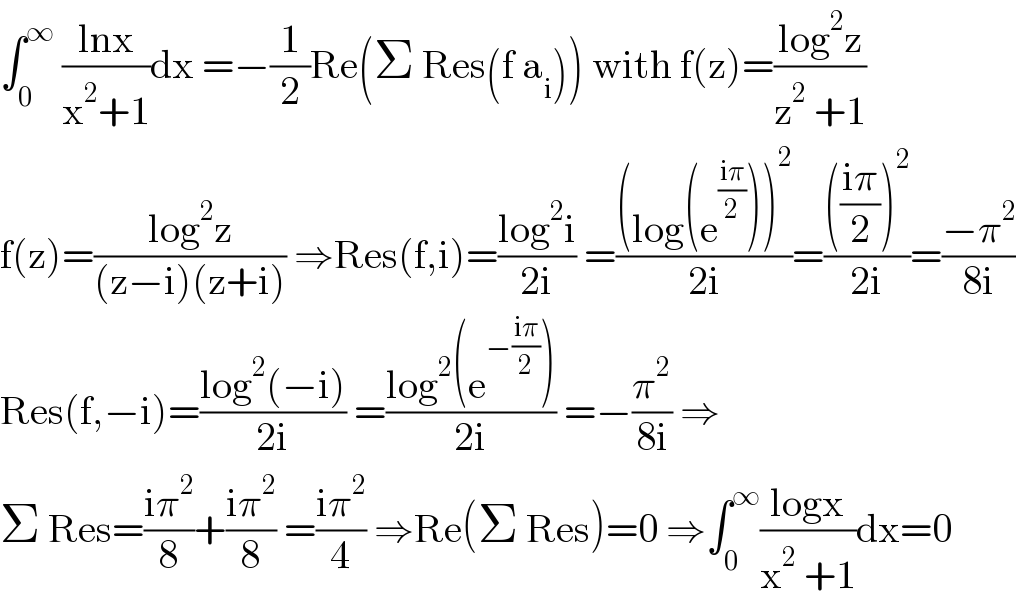
∫_0 ^∞ ((lnx)/(x^2 +1))dx =−(1/2)Re(Σ Res(f a_i )) with f(z)=((log^2 z)/(z^2 +1)) f(z)=((log^2 z)/((z−i)(z+i))) ⇒Res(f,i)=((log^2 i)/(2i)) =(((log(e^((iπ)/2) ))^2 )/(2i))=(((((iπ)/2))^2 )/(2i))=((−π^2 )/(8i)) Res(f,−i)=((log^2 (−i))/(2i)) =((log^2 (e^(−((iπ)/2)) ))/(2i)) =−(π^2 /(8i)) ⇒ Σ Res=((iπ^2 )/8)+((iπ^2 )/8) =((iπ^2 )/4) ⇒Re(Σ Res)=0 ⇒∫_0 ^∞ ((logx)/(x^2 +1))dx=0

$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\Sigma\:\mathrm{Res}\left(\mathrm{f}\:\mathrm{a}_{\mathrm{i}} \right)\right)\:\mathrm{with}\:\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{log}^{\mathrm{2}} \mathrm{z}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{log}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}−\mathrm{i}\right)\left(\mathrm{z}+\mathrm{i}\right)}\:\Rightarrow\mathrm{Res}\left(\mathrm{f},\mathrm{i}\right)=\frac{\mathrm{log}^{\mathrm{2}} \mathrm{i}}{\mathrm{2i}}\:=\frac{\left(\mathrm{log}\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)\right)^{\mathrm{2}} }{\mathrm{2i}}=\frac{\left(\frac{\mathrm{i}\pi}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2i}}=\frac{−\pi^{\mathrm{2}} }{\mathrm{8i}} \\ $$$$\mathrm{Res}\left(\mathrm{f},−\mathrm{i}\right)=\frac{\mathrm{log}^{\mathrm{2}} \left(−\mathrm{i}\right)}{\mathrm{2i}}\:=\frac{\mathrm{log}^{\mathrm{2}} \left(\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)}{\mathrm{2i}}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{8i}}\:\Rightarrow \\ $$$$\Sigma\:\mathrm{Res}=\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{8}}+\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{8}}\:=\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow\mathrm{Re}\left(\Sigma\:\mathrm{Res}\right)=\mathrm{0}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{logx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com