
Question Number 188192 by universe last updated on 26/Feb/23
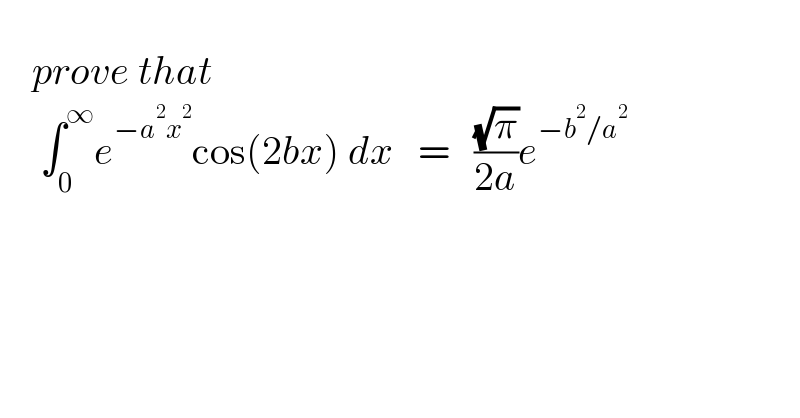
$$\:\:\: \\ $$$$\:\:\:\:{prove}\:{that} \\ $$$$\:\:\:\:\:\int_{\mathrm{0}} ^{\infty} {e}^{−{a}^{\mathrm{2}} {x}^{\mathrm{2}} } \mathrm{cos}\left(\mathrm{2}{bx}\right)\:{dx}\:\:\:=\:\:\:\frac{\sqrt{\pi}}{\mathrm{2}{a}}{e}^{−{b}^{\mathrm{2}} /{a}^{\mathrm{2}} } \\ $$$$ \\ $$$$ \\ $$
Answered by qaz last updated on 26/Feb/23

$${I}\left({b}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{a}^{\mathrm{2}} {x}^{\mathrm{2}} } \mathrm{cos}\:\left(\mathrm{2}{bx}\right){dx} \\ $$$${I}\left({b}\right)'=−\int_{\mathrm{0}} ^{\infty} \mathrm{2}{xe}^{−{a}^{\mathrm{2}} {x}^{\mathrm{2}} } \mathrm{sin}\:\left(\mathrm{2}{bx}\right){dx}=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }{e}^{−{a}^{\mathrm{2}} {x}^{\mathrm{2}} } \mathrm{sin}\:\left(\mathrm{2}{bx}\right)\mid_{\mathrm{0}} ^{\infty} −\frac{\mathrm{2}{b}}{{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} {e}^{−{a}^{\mathrm{2}} {x}^{\mathrm{2}} } \mathrm{cos}\:\left(\mathrm{2}{bx}\right){dx} \\ $$$$\Rightarrow{I}\left({b}\right)'=−\frac{\mathrm{2}{b}}{{a}^{\mathrm{2}} }{I}\left({b}\right)\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{I}\left({b}\right)={Ce}^{−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \\ $$$${C}={I}\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{a}^{\mathrm{2}} {x}^{\mathrm{2}} } {dx}=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}\left({a}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }=\frac{\sqrt{\pi}}{\mathrm{2}{a}}\:\:\:\:,{a}>\mathrm{0} \\ $$$$\Rightarrow{I}\left({b}\right)=\frac{\sqrt{\pi}}{\mathrm{2}{a}}{e}^{−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \:\:\:\:\:,{a}>\mathrm{0} \\ $$
Commented by universe last updated on 26/Feb/23

$${thanks}\:{sir} \\ $$
Answered by ARUNG_Brandon_MBU last updated on 26/Feb/23
![Ω=∫_0 ^∞ e^(−a^2 x^2 ) cos(2bx)dx =(1/2)Re∫_(−∞) ^∞ e^(−(a^2 x^2 +2ibx)) dx =(1/2)Re∫_(−∞) ^∞ e^(−[a^2 (x+((ib)/a^2 ))^2 +(b^2 /a^2 )]) dx =(1/2)Re{e^(−(b^2 /a^2 )) ∫_(−∞) ^∞ e^(−(ax+((ib)/a))^2 ) dx} =(1/2)Re{e^(−(b^2 /a^2 )) (1/a)∫_(−∞) ^∞ e^(−u^2 ) du}=((√π)/(2a))e^(−(b^2 /a^2 ))](Q188194.png)
$$\Omega=\int_{\mathrm{0}} ^{\infty} {e}^{−{a}^{\mathrm{2}} {x}^{\mathrm{2}} } \mathrm{cos}\left(\mathrm{2}{bx}\right){dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}{Re}\int_{−\infty} ^{\infty} {e}^{−\left({a}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{2}{ibx}\right)} {dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}{Re}\int_{−\infty} ^{\infty} {e}^{−\left[{a}^{\mathrm{2}} \left({x}+\frac{{ib}}{{a}^{\mathrm{2}} }\right)^{\mathrm{2}} +\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right]} {dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}{Re}\left\{{e}^{−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \int_{−\infty} ^{\infty} {e}^{−\left({ax}+\frac{{ib}}{{a}}\right)^{\mathrm{2}} } {dx}\right\} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}{Re}\left\{{e}^{−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \frac{\mathrm{1}}{{a}}\int_{−\infty} ^{\infty} {e}^{−{u}^{\mathrm{2}} } {du}\right\}=\frac{\sqrt{\pi}}{\mathrm{2}{a}}{e}^{−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \\ $$
