
Question Number 203921 by Davidtim last updated on 02/Feb/24
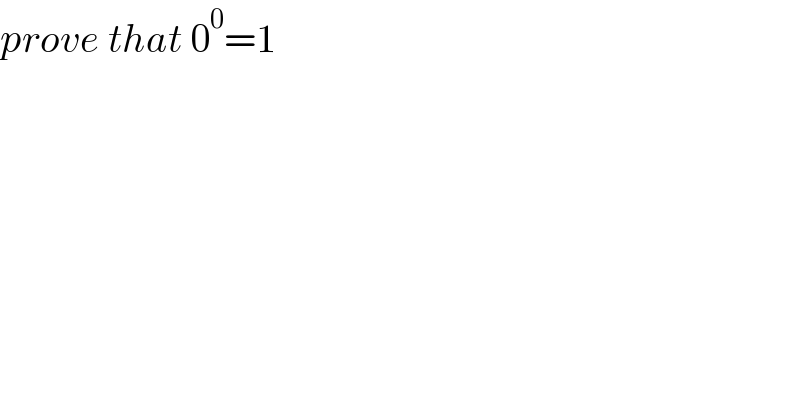
$${prove}\:{that}\:\mathrm{0}^{\mathrm{0}} =\mathrm{1} \\ $$
Commented by malwan last updated on 02/Feb/24

$${this}\:{is}\:{indeterminate}\:{form} \\ $$$${but}\:\underset{{x}\rightarrow\mathrm{0}^{+} } {{lim}}\:{x}^{{x}} \:=\:\mathrm{1} \\ $$
Commented by MATHEMATICSAM last updated on 02/Feb/24
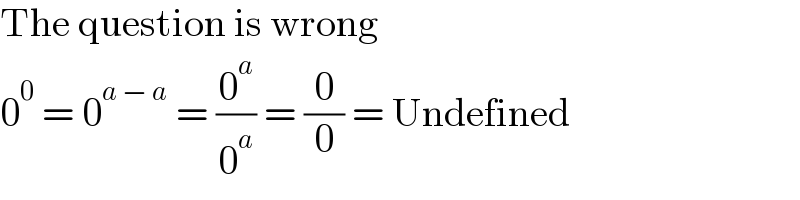
$$\mathrm{The}\:\mathrm{question}\:\mathrm{is}\:\mathrm{wrong} \\ $$$$\mathrm{0}^{\mathrm{0}} \:=\:\mathrm{0}^{{a}\:−\:{a}} \:=\:\frac{\mathrm{0}^{{a}} }{\mathrm{0}^{{a}} }\:=\:\frac{\mathrm{0}}{\mathrm{0}}\:=\:\mathrm{Undefined} \\ $$
Commented by siyathokoza last updated on 06/Feb/24

$$\mathrm{The}\:\mathrm{question}\:\mathrm{is}\:\mathrm{wrong} \\ $$$$\mathrm{0}^{\mathrm{0}} \:=\:\mathrm{0}^{{a}\:−\:{a}} \:=\:\frac{\mathrm{0}^{{a}} }{\mathrm{0}^{{a}} }\:=\:\frac{\mathrm{0}}{\mathrm{0}}\:=\:\mathrm{Undefined} \\ $$$$ \\ $$$$ \\ $$$${third}\:{floor}\:\mathrm{4}\:{upwards}\:{from}\:\mathrm{101} \\ $$$$ \\ $$$$ \\ $$
