
Question Number 215516 by MrGaster last updated on 09/Jan/25
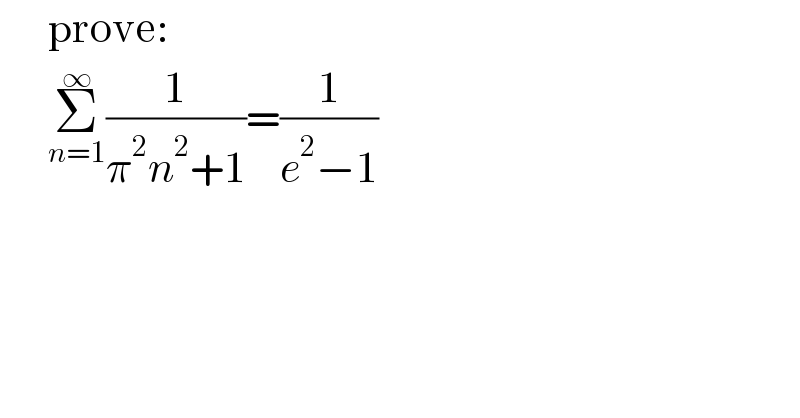
$$\:\:\:\:\:\:\mathrm{prove}: \\ $$$$\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\pi^{\mathrm{2}} {n}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{{e}^{\mathrm{2}} −\mathrm{1}} \\ $$
Answered by mr W last updated on 09/Jan/25
![Σ_(n=1) ^∞ (1/(π^2 n^2 +1)) =(1/(2i))Σ_(n=1) ^∞ ((1/(πn−i))−(1/(πn+i))) =(1/(2πi))Σ_(n=1) ^∞ ((1/(n−(i/π)))−(1/(π+(i/π)))) =(1/(2πi))[Σ_(n=1) ^∞ (1/n)−γ−ψ(1−(i/π))−Σ_(n=1) ^∞ (1/n)+γ+ψ(1+(i/π))] =(1/(2πi))[ψ(1+(i/π))−ψ(1−(i/π))] =(1/(2πi))[ψ((i/π))+(π/i)−ψ((i/π))−π cot i] =(1/(2πi))((π/i)−π cot i) =(1/(2πi))((π/i)−(π/i)coth 1) =(1/2)(coth 1−1) =(1/2)(((e+e^(−1) )/(e−e^(−1) ))−1) =(e^(−1) /(e−e^(−1) )) =(1/(e^2 −1)) ✓](Q215517.png)
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\pi^{\mathrm{2}} {n}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\pi{n}−{i}}−\frac{\mathrm{1}}{\pi{n}+{i}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}−\frac{{i}}{\pi}}−\frac{\mathrm{1}}{\pi+\frac{{i}}{\pi}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi{i}}\left[\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\gamma−\psi\left(\mathrm{1}−\frac{{i}}{\pi}\right)−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}+\gamma+\psi\left(\mathrm{1}+\frac{{i}}{\pi}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi{i}}\left[\psi\left(\mathrm{1}+\frac{{i}}{\pi}\right)−\psi\left(\mathrm{1}−\frac{{i}}{\pi}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi{i}}\left[\psi\left(\frac{{i}}{\pi}\right)+\frac{\pi}{{i}}−\psi\left(\frac{{i}}{\pi}\right)−\pi\:\mathrm{cot}\:{i}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi{i}}\left(\frac{\pi}{{i}}−\pi\:\mathrm{cot}\:{i}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi{i}}\left(\frac{\pi}{{i}}−\frac{\pi}{{i}}\mathrm{coth}\:\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{coth}\:\mathrm{1}−\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{e}+{e}^{−\mathrm{1}} }{{e}−{e}^{−\mathrm{1}} }−\mathrm{1}\right) \\ $$$$=\frac{{e}^{−\mathrm{1}} }{{e}−{e}^{−\mathrm{1}} } \\ $$$$=\frac{\mathrm{1}}{{e}^{\mathrm{2}} −\mathrm{1}}\:\checkmark \\ $$
Commented by ajfour last updated on 10/Jan/25
https://youtu.be/dvzKfeWOqyw?si=EggqbIQMc8QTN9F6 LCR Series circuit current and voltages discussed.
Commented by MrGaster last updated on 09/Jan/25

$$\mathrm{Than}\Bbbk\:\mathrm{you}\:\mathrm{sir}. \\ $$
