
Question Number 197808 by mokys last updated on 29/Sep/23
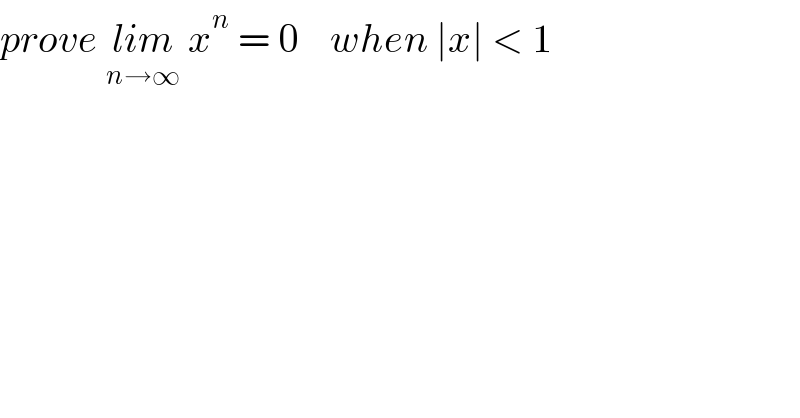
$${prove}\:\underset{{n}\rightarrow\infty} {{lim}}\:{x}^{{n}} \:=\:\mathrm{0}\:\:\:\:{when}\:\mid{x}\mid\:<\:\mathrm{1} \\ $$
Commented by Noorzai last updated on 30/Sep/23
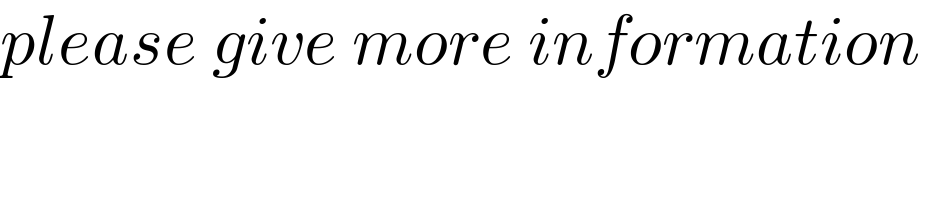
$${please}\:{give}\:{more}\:{information}\: \\ $$
Answered by mr W last updated on 30/Sep/23
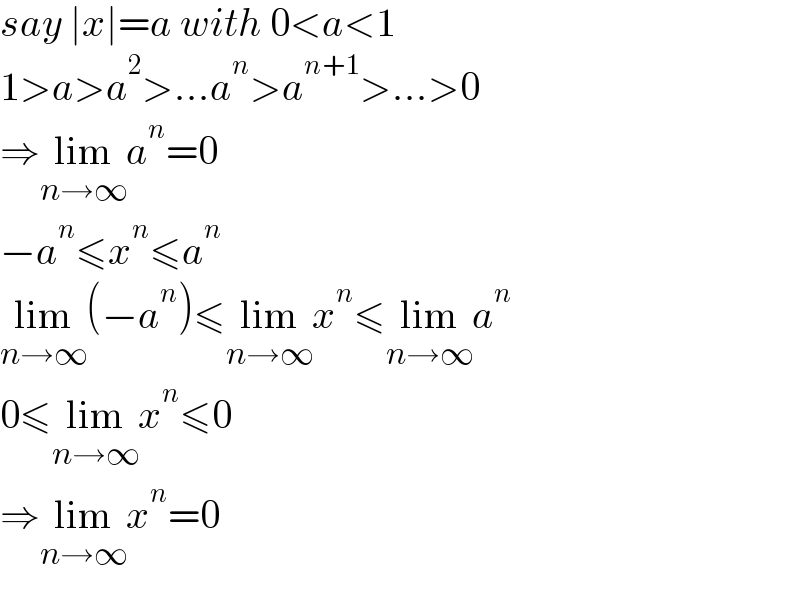
$${say}\:\mid{x}\mid={a}\:{with}\:\mathrm{0}<{a}<\mathrm{1} \\ $$$$\mathrm{1}>{a}>{a}^{\mathrm{2}} >...{a}^{{n}} >{a}^{{n}+\mathrm{1}} >...>\mathrm{0} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}^{{n}} =\mathrm{0} \\ $$$$−{a}^{{n}} \leqslant{x}^{{n}} \leqslant{a}^{{n}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(−{a}^{{n}} \right)\leqslant\underset{{n}\rightarrow\infty} {\mathrm{lim}}{x}^{{n}} \leqslant\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}^{{n}} \\ $$$$\mathrm{0}\leqslant\underset{{n}\rightarrow\infty} {\mathrm{lim}}{x}^{{n}} \leqslant\mathrm{0} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}{x}^{{n}} =\mathrm{0} \\ $$
Commented by mokys last updated on 30/Sep/23

$${thank}\:{you}\: \\ $$
