
Question Number 192062 by mehdee42 last updated on 07/May/23
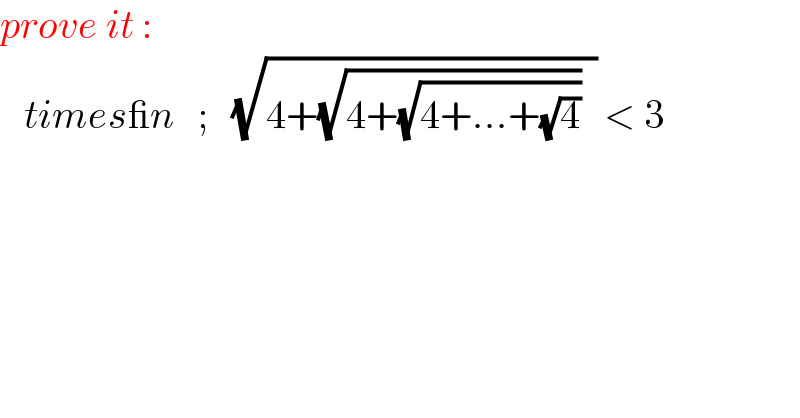
$${prove}\:{it}\::\: \\ $$$$\:\:\:{times\_n}\:\:\:;\:\:\:\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+...+\sqrt{\mathrm{4}}}}\:\:}\:<\:\mathrm{3} \\ $$
Commented by ajfour last updated on 08/May/23
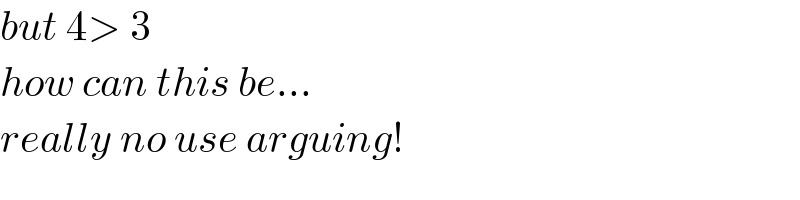
$${but}\:\mathrm{4}>\:\mathrm{3}\:\:\:\: \\ $$$${how}\:{can}\:{this}\:{be}... \\ $$$${really}\:{no}\:{use}\:{arguing}! \\ $$
Commented by ajfour last updated on 08/May/23
sometimes it just really dont make no sense et al.
Commented by mehdee42 last updated on 08/May/23

$${pay}\:{attention}\:{to}\:{question}\:\:\: \\ $$$${that}\:{is}\:\left(\sqrt{\mathrm{4}}<\mathrm{3}\:\right)\:{right}\:,\:{not}\:{what}\:{you}\:{wrote}\:\left(\mathrm{4}>\mathrm{3}\right) \\ $$
Answered by Frix last updated on 07/May/23
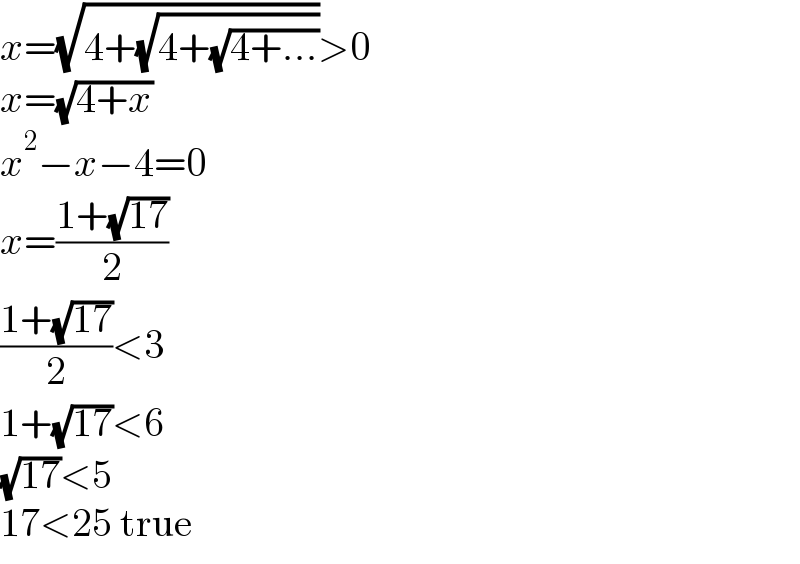
$${x}=\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+...}}}>\mathrm{0} \\ $$$${x}=\sqrt{\mathrm{4}+{x}} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{4}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{2}}<\mathrm{3} \\ $$$$\mathrm{1}+\sqrt{\mathrm{17}}<\mathrm{6} \\ $$$$\sqrt{\mathrm{17}}<\mathrm{5} \\ $$$$\mathrm{17}<\mathrm{25}\:\mathrm{true} \\ $$
Commented by mehdee42 last updated on 07/May/23

$${pay}\:\:{attention}\:: \\ $$$$\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+....}}}\:\neq\:\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+...\sqrt{\mathrm{4}}}}}\: \\ $$$$\Rightarrow\:{if}\:\:\:{x}=\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+...\sqrt{\mathrm{4}}}}}\nRightarrow{x}^{\mathrm{2}} =\mathrm{4}+{x} \\ $$$${the}\:{expression}\:{on}\:{the}\:{left}\:{contains}\:{the}\:{infinitive}\:{of}\:{the}\: \\ $$$${sentence}\:.{while}\:{the}\:{number}\:{of}\:\:{sentenes}\: \\ $$$${in}\:{thr}\:{right}\:{experession}\:{is}\:{finit}. \\ $$
Commented by Frix last updated on 07/May/23
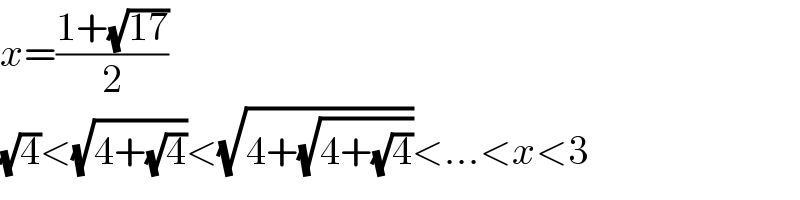
$${x}=\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$$\sqrt{\mathrm{4}}<\sqrt{\mathrm{4}+\sqrt{\mathrm{4}}}<\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+\sqrt{\mathrm{4}}}}<...<{x}<\mathrm{3} \\ $$
Commented by mehdee42 last updated on 07/May/23

$${why}\:\:``...<\:{x}\:<\mathrm{3}\:''\:?! \\ $$
Commented by deleteduser1 last updated on 07/May/23
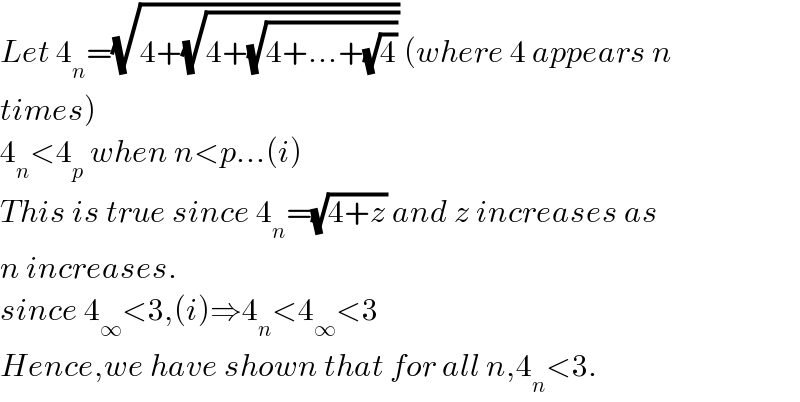
$${Let}\:\mathrm{4}_{{n}} =\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+...+\sqrt{\mathrm{4}}}}}\:\left({where}\:\mathrm{4}\:{appears}\:{n}\right. \\ $$$$\left.{times}\right) \\ $$$$\mathrm{4}_{{n}} <\mathrm{4}_{{p}} \:{when}\:{n}<{p}...\left({i}\right) \\ $$$${This}\:{is}\:{true}\:{since}\:\mathrm{4}_{{n}} =\sqrt{\mathrm{4}+{z}}\:{and}\:{z}\:{increases}\:{as} \\ $$$${n}\:{increases}. \\ $$$${since}\:\mathrm{4}_{\infty} <\mathrm{3},\left({i}\right)\Rightarrow\mathrm{4}_{{n}} <\mathrm{4}_{\infty} <\mathrm{3} \\ $$$${Hence},{we}\:{have}\:{shown}\:{that}\:{for}\:{all}\:{n},\mathrm{4}_{{n}} <\mathrm{3}. \\ $$
Commented by mehdee42 last updated on 07/May/23

$${sir} \\ $$$${why}\:\:\mathrm{4}_{{n}} <\mathrm{4}_{\infty} <\mathrm{3}\:\:?? \\ $$
Commented by mehdee42 last updated on 07/May/23

$${it}\:{can}\:{be}\:{proven}\:{by}\:{a}\:{very}\:{simple}\: \\ $$$${mahematical}\:{induction}\:{metod} \\ $$$${good}\:{luck} \\ $$
Answered by mehdee42 last updated on 08/May/23

$${answer}\:{to}\:{question}\:{number}\: \\ $$$${let}\::\:{p}_{{n}} =\:{n\_}\:{termes}\:\:\:\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+...+\sqrt{\mathrm{4}}}}\:}<\mathrm{3} \\ $$$$\:{p}_{\mathrm{1}} \:=\sqrt{\mathrm{4}}=\mathrm{2}<\mathrm{3}\:\checkmark\:\:\:\:\:\:{i}.{s} \\ $$$${p}_{{k}} \:=\:\left({k}\:\_\:{termes}\:\right)\:\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+....+\sqrt{\mathrm{4}}}}}<\mathrm{3}\:\:\:\:{i}.{h}\: \\ $$$${p}_{{k}+\mathrm{1}} \:=\left({k}+\mathrm{1}\:\_\:{termes}\right)\:\:\:\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+...+\sqrt{\mathrm{4}}}}}\:<\mathrm{3}\:\:\:?\:\:{i}.{r} \\ $$$${p}_{{k}+\mathrm{1}} ^{\mathrm{2}} \:=\mathrm{4}+\left({k\_termes}\right)\:\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+\sqrt{\mathrm{4}+...+\sqrt{\mathrm{4}}}}\:}<\mathrm{4}+\mathrm{3}=\mathrm{7}\: \\ $$$$\Rightarrow\:{p}_{{k}+\mathrm{1}} <\sqrt{\mathrm{7}}<\mathrm{3}\:\checkmark \\ $$$$ \\ $$
