
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 185659 by mr W last updated on 25/Jan/23
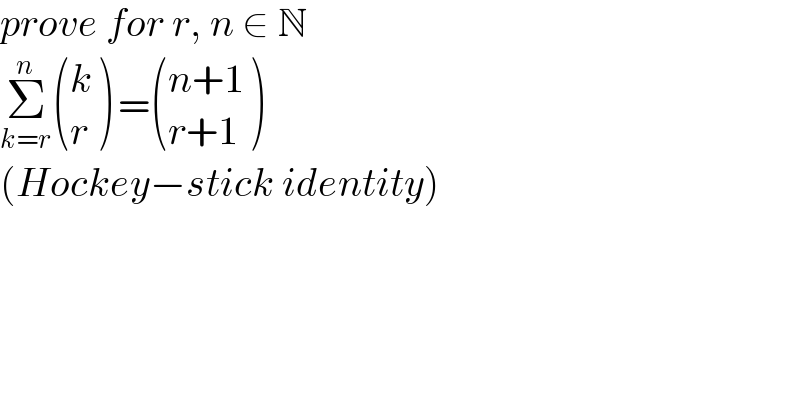
$${prove}\:{for}\:{r},\:{n}\:\in\:\mathbb{N} \\ $$$$\underset{{k}={r}} {\overset{{n}} {\sum}}\begin{pmatrix}{{k}}\\{{r}}\end{pmatrix}\:=\begin{pmatrix}{{n}+\mathrm{1}}\\{{r}+\mathrm{1}}\end{pmatrix} \\ $$$$\left({Hockey}−{stick}\:{identity}\right) \\ $$
Commented by mr W last updated on 25/Jan/23

Answered by mr W last updated on 25/Jan/23
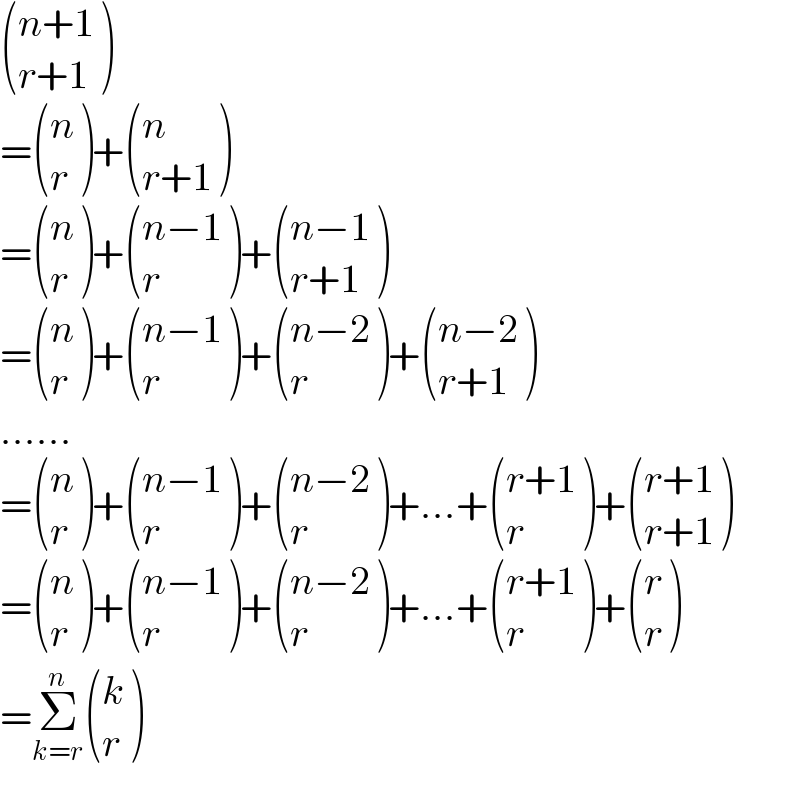
$$\begin{pmatrix}{{n}+\mathrm{1}}\\{{r}+\mathrm{1}}\end{pmatrix}\: \\ $$$$=\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}+\begin{pmatrix}{{n}}\\{{r}+\mathrm{1}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}+\begin{pmatrix}{{n}−\mathrm{1}}\\{{r}}\end{pmatrix}+\begin{pmatrix}{{n}−\mathrm{1}}\\{{r}+\mathrm{1}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}+\begin{pmatrix}{{n}−\mathrm{1}}\\{{r}}\end{pmatrix}+\begin{pmatrix}{{n}−\mathrm{2}}\\{{r}}\end{pmatrix}+\begin{pmatrix}{{n}−\mathrm{2}}\\{{r}+\mathrm{1}}\end{pmatrix} \\ $$$$...... \\ $$$$=\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}+\begin{pmatrix}{{n}−\mathrm{1}}\\{{r}}\end{pmatrix}+\begin{pmatrix}{{n}−\mathrm{2}}\\{{r}}\end{pmatrix}+...+\begin{pmatrix}{{r}+\mathrm{1}}\\{{r}}\end{pmatrix}+\begin{pmatrix}{{r}+\mathrm{1}}\\{{r}+\mathrm{1}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}+\begin{pmatrix}{{n}−\mathrm{1}}\\{{r}}\end{pmatrix}+\begin{pmatrix}{{n}−\mathrm{2}}\\{{r}}\end{pmatrix}+...+\begin{pmatrix}{{r}+\mathrm{1}}\\{{r}}\end{pmatrix}+\begin{pmatrix}{{r}}\\{{r}}\end{pmatrix} \\ $$$$=\underset{{k}={r}} {\overset{{n}} {\sum}}\begin{pmatrix}{{k}}\\{{r}}\end{pmatrix} \\ $$
Commented by cortano1 last updated on 25/Jan/23

$${yes}...{great} \\ $$
