
Question Number 117903 by aurpeyz last updated on 14/Oct/20
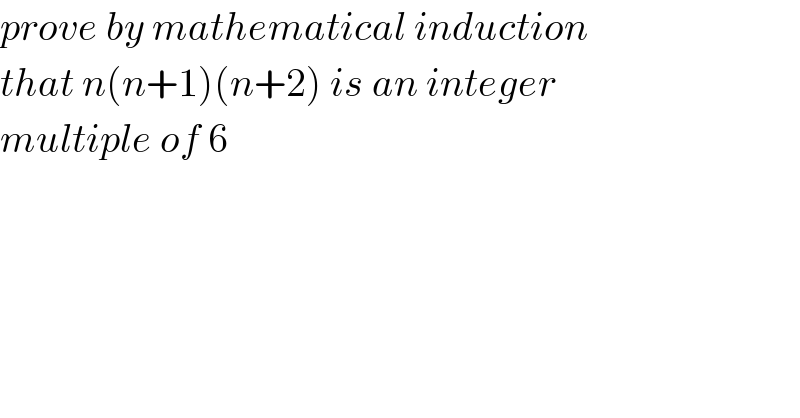
$${prove}\:{by}\:{mathematical}\:{induction} \\ $$$${that}\:{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\:{is}\:{an}\:{integer}\: \\ $$$${multiple}\:{of}\:\mathrm{6} \\ $$
Answered by mindispower last updated on 14/Oct/20
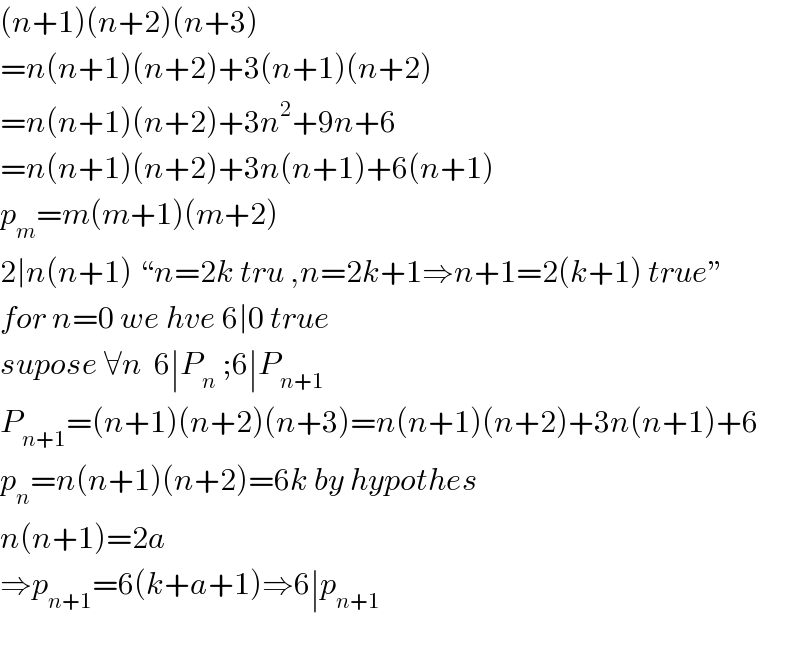
$$\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right) \\ $$$$={n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)+\mathrm{3}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right) \\ $$$$={n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)+\mathrm{3}{n}^{\mathrm{2}} +\mathrm{9}{n}+\mathrm{6} \\ $$$$={n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)+\mathrm{3}{n}\left({n}+\mathrm{1}\right)+\mathrm{6}\left({n}+\mathrm{1}\right) \\ $$$${p}_{{m}} ={m}\left({m}+\mathrm{1}\right)\left({m}+\mathrm{2}\right) \\ $$$$\mathrm{2}\mid{n}\left({n}+\mathrm{1}\right)\:``{n}=\mathrm{2}{k}\:{tru}\:,{n}=\mathrm{2}{k}+\mathrm{1}\Rightarrow{n}+\mathrm{1}=\mathrm{2}\left({k}+\mathrm{1}\right)\:{true}'' \\ $$$${for}\:{n}=\mathrm{0}\:{we}\:{hve}\:\mathrm{6}\mid\mathrm{0}\:{true} \\ $$$${supose}\:\forall{n}\:\:\mathrm{6}\mid{P}_{{n}} \:;\mathrm{6}\mid{P}_{{n}+\mathrm{1}} \\ $$$${P}_{{n}+\mathrm{1}} =\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)={n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)+\mathrm{3}{n}\left({n}+\mathrm{1}\right)+\mathrm{6} \\ $$$${p}_{{n}} ={n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)=\mathrm{6}{k}\:{by}\:{hypothes} \\ $$$${n}\left({n}+\mathrm{1}\right)=\mathrm{2}{a} \\ $$$$\Rightarrow{p}_{{n}+\mathrm{1}} =\mathrm{6}\left({k}+{a}+\mathrm{1}\right)\Rightarrow\mathrm{6}\mid{p}_{{n}+\mathrm{1}} \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 14/Oct/20

$$\mathrm{Prove}\:\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)\:\mathrm{is}\:\mathrm{multiply}\:\mathrm{of}\:\mathrm{6} \\ $$$$\forall\mathrm{n}\in\mathrm{N},\mathrm{n}\geqslant\mathrm{1by}\:\mathrm{mathematical}\:\mathrm{inuction} \\ $$$$\left.\mathrm{i}\right)\mathrm{For}\:\mathrm{n}=\mathrm{1}\Rightarrow\mathrm{A}_{\mathrm{1}} =\mathrm{1}.\mathrm{2}.\mathrm{3}=\mathrm{6}\vdots\mathrm{6}\Rightarrow\mathrm{State}\:\mathrm{is}\:\mathrm{true} \\ $$$$\left.\mathrm{ii}\right)\mathrm{Suppose}\:\mathrm{State}\:\mathrm{was}\:\mathrm{true}\:\forall\mathrm{n}\leqslant\mathrm{k} \\ $$$$\mathrm{that}\:\mathrm{means}\:\mathrm{A}_{\mathrm{k}} =\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)\vdots\mathrm{6} \\ $$$$\left.\mathrm{iii}\right)\mathrm{We}\:\mathrm{will}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{A}_{\mathrm{k}+\mathrm{1}} \vdots\mathrm{6} \\ $$$$\mathrm{Indeed},\mathrm{A}_{\mathrm{k}+\mathrm{1}} =\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)\left(\mathrm{k}+\mathrm{3}\right) \\ $$$$=\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)+\mathrm{3}\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right) \\ $$$$=\mathrm{A}_{\mathrm{k}} +\mathrm{3}\left(\mathrm{k}^{\mathrm{2}} +\mathrm{3k}+\mathrm{2}\right)=\mathrm{A}_{\mathrm{k}} +\mathrm{3k}\left(\mathrm{k}+\mathrm{1}\right) \\ $$$$+\mathrm{6}\left(\mathrm{k}+\mathrm{1}\right)\vdots\mathrm{6}\:\mathrm{Since}\:\mathrm{A}_{\mathrm{k}} \vdots\mathrm{6},\mathrm{6}\left(\mathrm{k}+\mathrm{1}\right)\vdots\mathrm{6} \\ $$$$\mathrm{3k}\left(\mathrm{k}+\mathrm{1}\right)\vdots\mathrm{6}\left(\mathrm{by}\:\mathrm{in}\:\mathrm{two}\:\mathrm{sequence}\:\mathrm{numbers}\right. \\ $$$$\left.\mathrm{always}\:\mathrm{have}\:\mathrm{one}\:\mathrm{even}\:\mathrm{number}\:\right) \\ $$$$\mathrm{Thus},\mathrm{State}\:\mathrm{is}\:\mathrm{also}\:\mathrm{for}\:\mathrm{n}=\mathrm{k}+\mathrm{1},\mathrm{so} \\ $$$$\mathrm{by}\:\mathrm{mathimatical}\:\:\mathrm{induction}\:\mathrm{principle} \\ $$$$\mathrm{State}\:\mathrm{is}\:\mathrm{true}\:\forall\mathrm{n}\in\mathrm{N}^{\ast} \left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right) \\ $$
