
Question Number 78333 by Lontum Hans last updated on 16/Jan/20

$$\mathrm{prove}\:\mathrm{by}\:\mathrm{contradiction}\:\mathrm{that}\:\sqrt{\mathrm{2}\:}\:\mathrm{is}\:\mathrm{irrational}. \\ $$
Answered by MJS last updated on 16/Jan/20
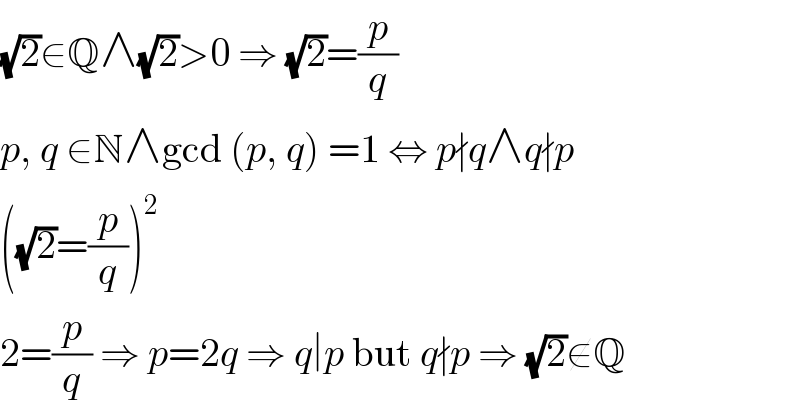
$$\sqrt{\mathrm{2}}\in\mathbb{Q}\wedge\sqrt{\mathrm{2}}>\mathrm{0}\:\Rightarrow\:\sqrt{\mathrm{2}}=\frac{{p}}{{q}} \\ $$$${p},\:{q}\:\in\mathbb{N}\wedge\mathrm{gcd}\:\left({p},\:{q}\right)\:=\mathrm{1}\:\Leftrightarrow\:{p}\nmid{q}\wedge{q}\nmid{p} \\ $$$$\left(\sqrt{\mathrm{2}}=\frac{{p}}{{q}}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}=\frac{{p}}{{q}}\:\Rightarrow\:{p}=\mathrm{2}{q}\:\Rightarrow\:{q}\mid{p}\:\mathrm{but}\:{q}\nmid{p}\:\Rightarrow\:\sqrt{\mathrm{2}}\notin\mathbb{Q} \\ $$
