
Question Number 152345 by mnjuly1970 last updated on 27/Aug/21
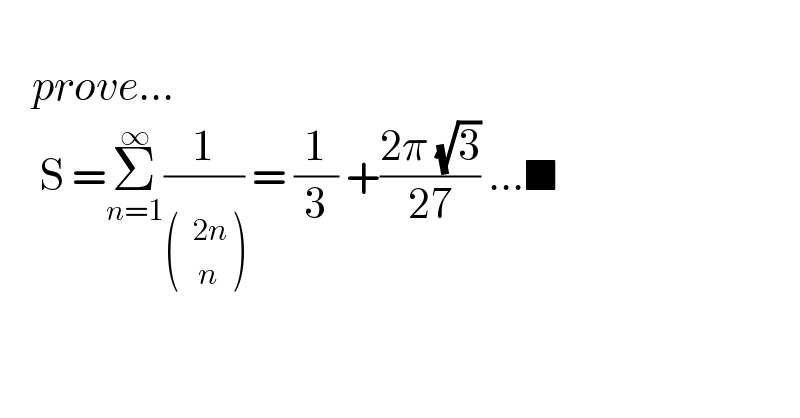
$$ \\ $$$$\:\:\:\:{prove}... \\ $$$$\:\:\:\:\:\mathrm{S}\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{2}\pi\:\sqrt{\mathrm{3}}}{\mathrm{27}}\:...\blacksquare \\ $$$$ \\ $$
Answered by Kamel last updated on 27/Aug/21
![prove... S =Σ_(n=1) ^∞ (1/) = (1/3) +((2π (√3))/(27)) ...■ =Σ_(n=1) ^(+∞) ((nΓ(n+1)Γ(n))/(Γ(2n+1)))=Σ_(n=1) ^(+∞) n∫_0 ^1 t^(n−1) (1−t)^n dt =∫_0 ^1 (d/dy)[Σ_(n=1) ^(+∞) y^n (1−t)^n ]_(y=t) dt=∫_0 ^1 ((1−t)/((1−t(1−t))^2 ))dt =∫_0 ^1 (u/((u^2 −u+1)^2 ))du=∫_1 ^(+∞) (u/((u^2 −u+1)^2 ))du S=(1/2)∫_0 ^(+∞) ((udu)/((u^2 −u+1)^2 )) =(1/2)(d/da)[∫_0 ^(+∞) (du/((u^2 −au+1)))]_(a=1) =(1/2)(d/da)[(1/( (√(1−(a^2 /4)))))((π/2)+Arctan((a/( 2(√(1−(a^2 /4)))))))]_(a=1) =(1/2)[ (2/(3(√3)))((π/2)+Arctan((1/( (√3)))))−(1/( 2(√3)))(((((−1)/( (√3)))−(√3))/4))] =((2π)/( 9(√3)))+(1/3)=(1/3)+((2π(√3))/(27))](Q152368.png)
$$ \\ $$$$\:\:\:\:{prove}... \\ $$$$\:\:\:\:\:\mathrm{S}\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{2}\pi\:\sqrt{\mathrm{3}}}{\mathrm{27}}\:...\blacksquare \\ $$$$\:\:\:\:\:\:=\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{{n}\Gamma\left({n}+\mathrm{1}\right)\Gamma\left({n}\right)}{\Gamma\left(\mathrm{2}{n}+\mathrm{1}\right)}=\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}{n}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{n}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{n}} {dt} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{d}}{{dy}}\left[\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}{y}^{{n}} \left(\mathrm{1}−{t}\right)^{{n}} \right]_{{y}={t}} {dt}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{t}}{\left(\mathrm{1}−{t}\left(\mathrm{1}−{t}\right)\right)^{\mathrm{2}} }{dt} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}}{\left({u}^{\mathrm{2}} −{u}+\mathrm{1}\right)^{\mathrm{2}} }{du}=\int_{\mathrm{1}} ^{+\infty} \frac{{u}}{\left({u}^{\mathrm{2}} −{u}+\mathrm{1}\right)^{\mathrm{2}} }{du} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{+\infty} \frac{{udu}}{\left({u}^{\mathrm{2}} −{u}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\frac{{d}}{{da}}\left[\int_{\mathrm{0}} ^{+\infty} \frac{{du}}{\left({u}^{\mathrm{2}} −{au}+\mathrm{1}\right)}\right]_{{a}=\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\frac{{d}}{{da}}\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}}\left(\frac{\pi}{\mathrm{2}}+{Arctan}\left(\frac{{a}}{\:\mathrm{2}\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}}\right)\right)\right]_{{a}=\mathrm{1}} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\:\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\left(\frac{\pi}{\mathrm{2}}+{Arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right)−\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{3}}}\left(\frac{\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}−\sqrt{\mathrm{3}}}{\mathrm{4}}\right)\right] \\ $$$$\:\:=\frac{\mathrm{2}\pi}{\:\mathrm{9}\sqrt{\mathrm{3}}}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}\pi\sqrt{\mathrm{3}}}{\mathrm{27}} \\ $$
Commented by mnjuly1970 last updated on 28/Aug/21
$${verh}\:{nice}\:{sir}\:{kamel}..{tashakor} \\ $$
