
Question Number 211245 by Ghisom last updated on 01/Sep/24
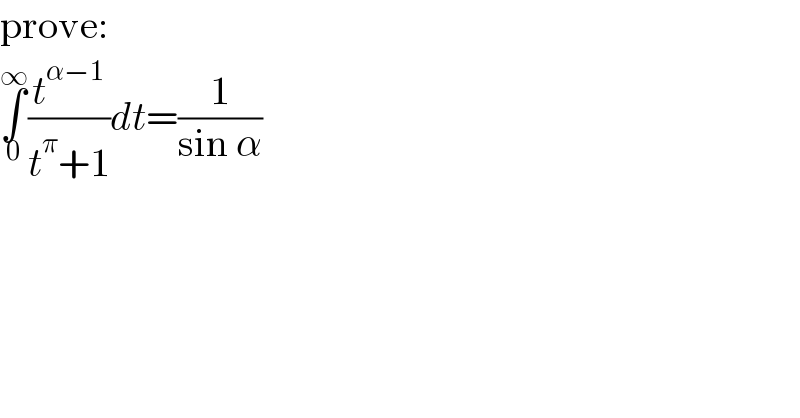
$$\mathrm{prove}: \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{t}^{\alpha−\mathrm{1}} }{{t}^{\pi} +\mathrm{1}}{dt}=\frac{\mathrm{1}}{\mathrm{sin}\:\alpha} \\ $$
Answered by Frix last updated on 02/Sep/24
![∫_0 ^∞ (t^(α−1) /(t^π +1))dt =^([u=t^π ]) (1/π)∫_0 ^∞ (u^((α/π)−1) /(u+1))du= =(1/π)∫_0 ^∞ (u^((α/π)−1) /((u+1)^((α/π)+(1−(α/π))) ))du= =(1/π)B ((α/π), 1−(α/π)) =((Γ ((α/π)) Γ (1−(α/π)))/(πΓ ((α/π)+(1−(α/π))))) =^([(α/π)=z]) =((Γ (z) Γ (1−z))/(πΓ (1)))=((πcsc (πz))/π) =^([z=(α/π)]) csc α = =(1/(sin α))](Q211253.png)
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{{t}^{\alpha−\mathrm{1}} }{{t}^{\pi} +\mathrm{1}}{dt}\:\overset{\left[{u}={t}^{\pi} \right]} {=}\:\frac{\mathrm{1}}{\pi}\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{{u}^{\frac{\alpha}{\pi}−\mathrm{1}} }{{u}+\mathrm{1}}{du}= \\ $$$$=\frac{\mathrm{1}}{\pi}\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{{u}^{\frac{\alpha}{\pi}−\mathrm{1}} }{\left({u}+\mathrm{1}\right)^{\frac{\alpha}{\pi}+\left(\mathrm{1}−\frac{\alpha}{\pi}\right)} }{du}= \\ $$$$=\frac{\mathrm{1}}{\pi}{B}\:\left(\frac{\alpha}{\pi},\:\mathrm{1}−\frac{\alpha}{\pi}\right)\:=\frac{\Gamma\:\left(\frac{\alpha}{\pi}\right)\:\Gamma\:\left(\mathrm{1}−\frac{\alpha}{\pi}\right)}{\pi\Gamma\:\left(\frac{\alpha}{\pi}+\left(\mathrm{1}−\frac{\alpha}{\pi}\right)\right)}\:\overset{\left[\frac{\alpha}{\pi}={z}\right]} {=} \\ $$$$=\frac{\Gamma\:\left({z}\right)\:\Gamma\:\left(\mathrm{1}−{z}\right)}{\pi\Gamma\:\left(\mathrm{1}\right)}=\frac{\pi\mathrm{csc}\:\left(\pi{z}\right)}{\pi}\:\overset{\left[{z}=\frac{\alpha}{\pi}\right]} {=}\:\mathrm{csc}\:\alpha\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{sin}\:\alpha} \\ $$
Commented by Ghisom last updated on 02/Sep/24

$$\mathrm{thank}\:\mathrm{you} \\ $$
