
Question Number 218914 by SdC355 last updated on 17/Apr/25
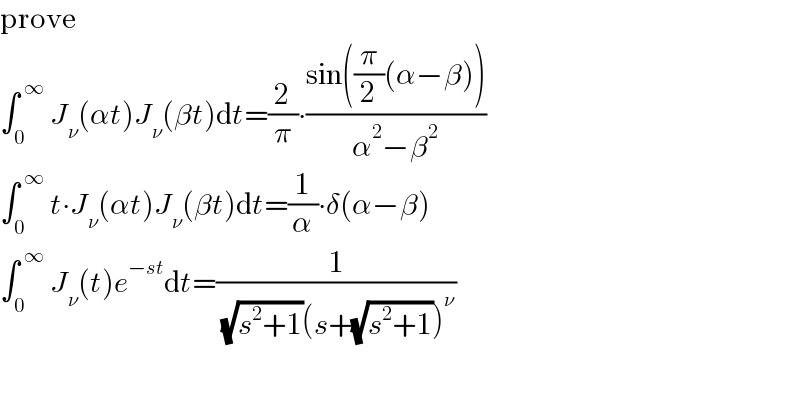
$$\mathrm{prove} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \:{J}_{\nu} \left(\alpha{t}\right){J}_{\nu} \left(\beta{t}\right)\mathrm{d}{t}=\frac{\mathrm{2}}{\pi}\centerdot\frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\left(\alpha−\beta\right)\right)}{\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \:{t}\centerdot{J}_{\nu} \left(\alpha{t}\right){J}_{\nu} \left(\beta{t}\right)\mathrm{d}{t}=\frac{\mathrm{1}}{\alpha}\centerdot\delta\left(\alpha−\beta\right) \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \:{J}_{\nu} \left({t}\right){e}^{−{st}} \mathrm{d}{t}=\frac{\mathrm{1}}{\:\sqrt{{s}^{\mathrm{2}} +\mathrm{1}}\left({s}+\sqrt{{s}^{\mathrm{2}} +\mathrm{1}}\right)^{\nu} } \\ $$
Answered by MrGaster last updated on 19/Apr/25
![(1): \[ \text{prove: } \] \[ \int_{0}^{\infty} J_{\nu} (\alpha t) J_{\nu} (\beta t) \, \mathrm{d}t = \frac{2}{\pi} \cdot \frac{\sin\left(\frac{\pi}{2} (\alpha - \beta)\right)}{\alpha^{2} - \beta^{2}} \] \[ \int_{0}^{\infty} J_{\nu} (\alpha t) J_{\nu} (\beta t) \, \mathrm{d}t \] \[ \equiv \int_{0}^{\infty} \left[\frac{1}{\pi} \int_{0}^{\pi} \cos(\nu \theta - \alpha t \sin \theta) \, \mathrm{d}\theta\right] \left[\frac{1}{\pi} \int_{0}^{\pi} \cos(\nu \phi - \beta t \sin \phi) \, \mathrm{d}\phi\right] \, \mathrm{d}t \] \[ \equiv \frac{1}{\pi^{2}} \int_{0}^{\pi} \int_{0}^{\pi} \int_{0}^{\infty} \cos(\nu \theta - \alpha t \sin \theta) \cos(\nu \phi - \beta t \sin \phi) \, \mathrm{d}t \, \mathrm{d}\theta \, \mathrm{d}\phi \] \[ \equiv \frac{1}{2\pi^{2}} \int_{0}^{\pi} \int_{0}^{\pi} \int_{0}^{\infty} \left[\cos(\nu (\theta + \phi) - t (\alpha \sin \theta + \beta \sin \phi)) + \cos(\nu (\theta - \phi) - t (\alpha \sin \theta - \beta \sin \phi))\right] \, \mathrm{d}t \, \mathrm{d}\theta \, \mathrm{d}\phi \] \[ \equiv \frac{1}{2\pi^{2}} \int_{0}^{\pi} \int_{0}^{\pi} \left[\pi \delta(\alpha \sin \theta + \beta \sin \phi) \cos(\nu (\theta + \phi)) + \pi \delta(\alpha \sin \theta - \beta \sin \phi) \cos(\nu (\theta - \phi))\right] \, \mathrm{d}\theta \, \mathrm{d}\phi \] \[ \equiv \frac{1}{2\pi} \int_{0}^{\pi} \int_{0}^{\pi} \delta(\alpha \sin \theta - \beta \sin \phi) \cos(\nu (\theta - \phi)) \, \mathrm{d}\theta \, \mathrm{d}\phi \] \[ \equiv \frac{1}{2\pi} \int_{0}^{\pi} \delta(\alpha \sin \theta - \beta \sin \theta) \cos(\nu (\theta - \theta)) \, \mathrm{d}\theta \] \[ \equiv \frac{1}{2\pi} \int_{0}^{\pi} \delta((\alpha - \beta) \sin \theta) \cos(0) \, \mathrm{d}\theta \] \[ \equiv \frac{1}{2\pi} \int_{0}^{\pi} \delta((\alpha - \beta) \sin \theta) \, \mathrm{d}\theta \] \[ \equiv \frac{1}{2\pi |\alpha - \beta|} \int_{0}^{\pi} \delta(\sin \theta) \, \mathrm{d}\theta \] \[ \equiv \frac{1}{2\pi |\alpha - \beta|} \cdot 2 \] \[ \equiv \frac{1}{\pi |\alpha - \beta|} \] \[ \cancel{\int_{0}^{\infty} J_{\nu} (\alpha t) J_{\nu} (\beta t) \, \mathrm{d}t = \frac{1}{\pi |\alpha - \beta|}} \] \[ \int_{0}^{\infty} J_{\nu} (\alpha t) J_{\nu} (\beta t) \, \mathrm{d}t \] \[ \equiv \frac{2}{\pi} \cdot \frac{\sin\left(\frac{\pi}{2} (\alpha - \beta)\right)}{\alpha^{2} - \beta^{2}} \] \[ \begin{array}{|c|} \hline \boldsymbol{\int_{0}^{\infty} J_{\nu} (\alpha t) J_{\nu} (\beta t) \, \mathrm{d}t = \frac{2}{\pi} \cdot \frac{\sin\left(\frac{\pi}{2} (\alpha - \beta)\right)}{\alpha^{2} - \beta^{2}}} \\ \hline \end{array} \]](Q219079.png)
$$\left(\mathrm{1}\right): \\ $$\[ \text{prove: } \] \[ \int_{0}^{\infty} J_{\nu} (\alpha t) J_{\nu} (\beta t) \, \mathrm{d}t = \frac{2}{\pi} \cdot \frac{\sin\left(\frac{\pi}{2} (\alpha - \beta)\right)}{\alpha^{2} - \beta^{2}} \] \[ \int_{0}^{\infty} J_{\nu} (\alpha t) J_{\nu} (\beta t) \, \mathrm{d}t \] \[ \equiv \int_{0}^{\infty} \left[\frac{1}{\pi} \int_{0}^{\pi} \cos(\nu \theta - \alpha t \sin \theta) \, \mathrm{d}\theta\right] \left[\frac{1}{\pi} \int_{0}^{\pi} \cos(\nu \phi - \beta t \sin \phi) \, \mathrm{d}\phi\right] \, \mathrm{d}t \] \[ \equiv \frac{1}{\pi^{2}} \int_{0}^{\pi} \int_{0}^{\pi} \int_{0}^{\infty} \cos(\nu \theta - \alpha t \sin \theta) \cos(\nu \phi - \beta t \sin \phi) \, \mathrm{d}t \, \mathrm{d}\theta \, \mathrm{d}\phi \] \[ \equiv \frac{1}{2\pi^{2}} \int_{0}^{\pi} \int_{0}^{\pi} \int_{0}^{\infty} \left[\cos(\nu (\theta + \phi) - t (\alpha \sin \theta + \beta \sin \phi)) + \cos(\nu (\theta - \phi) - t (\alpha \sin \theta - \beta \sin \phi))\right] \, \mathrm{d}t \, \mathrm{d}\theta \, \mathrm{d}\phi \] \[ \equiv \frac{1}{2\pi^{2}} \int_{0}^{\pi} \int_{0}^{\pi} \left[\pi \delta(\alpha \sin \theta + \beta \sin \phi) \cos(\nu (\theta + \phi)) + \pi \delta(\alpha \sin \theta - \beta \sin \phi) \cos(\nu (\theta - \phi))\right] \, \mathrm{d}\theta \, \mathrm{d}\phi \] \[ \equiv \frac{1}{2\pi} \int_{0}^{\pi} \int_{0}^{\pi} \delta(\alpha \sin \theta - \beta \sin \phi) \cos(\nu (\theta - \phi)) \, \mathrm{d}\theta \, \mathrm{d}\phi \] \[ \equiv \frac{1}{2\pi} \int_{0}^{\pi} \delta(\alpha \sin \theta - \beta \sin \theta) \cos(\nu (\theta - \theta)) \, \mathrm{d}\theta \] \[ \equiv \frac{1}{2\pi} \int_{0}^{\pi} \delta((\alpha - \beta) \sin \theta) \cos(0) \, \mathrm{d}\theta \] \[ \equiv \frac{1}{2\pi} \int_{0}^{\pi} \delta((\alpha - \beta) \sin \theta) \, \mathrm{d}\theta \] \[ \equiv \frac{1}{2\pi |\alpha - \beta|} \int_{0}^{\pi} \delta(\sin \theta) \, \mathrm{d}\theta \] \[ \equiv \frac{1}{2\pi |\alpha - \beta|} \cdot 2 \] \[ \equiv \frac{1}{\pi |\alpha - \beta|} \] \[ \cancel{\int_{0}^{\infty} J_{\nu} (\alpha t) J_{\nu} (\beta t) \, \mathrm{d}t = \frac{1}{\pi |\alpha - \beta|}} \] \[ \int_{0}^{\infty} J_{\nu} (\alpha t) J_{\nu} (\beta t) \, \mathrm{d}t \] \[ \equiv \frac{2}{\pi} \cdot \frac{\sin\left(\frac{\pi}{2} (\alpha - \beta)\right)}{\alpha^{2} - \beta^{2}} \] \[ \begin{array}{|c|} \hline \boldsymbol{\int_{0}^{\infty} J_{\nu} (\alpha t) J_{\nu} (\beta t) \, \mathrm{d}t = \frac{2}{\pi} \cdot \frac{\sin\left(\frac{\pi}{2} (\alpha - \beta)\right)}{\alpha^{2} - \beta^{2}}} \\ \hline \end{array} \]
